Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T17:57:08.967Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Solvability of a Neumann Boundary Value Problem at Resonance

Published online by Cambridge University Press:  20 November 2018

Chung-Cheng Kuo
Chung-Cheng Kuo*
Affiliation:
Department of Mathematics, Fu Jen University, Taipei, Taiwan
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the existence of solutions of the semilinear equations (1) 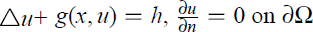in which the non-linearity g may grow superlinearly in u in one of directions u → ∞ and u → −∞, and (2) −Δu + g(x, u) = h, 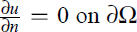in which the nonlinear term g may grow superlinearly in u as |u| → ∞. The purpose of this paper is to obtain solvability theorems for (1) and (2) when the Landesman-Lazer condition does not hold. More precisely, we require that h may satisfy 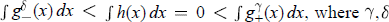are arbitrarily nonnegative constants, 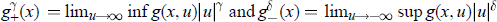. The proofs are based upon degree theoretic arguments.

Keywords

35J6547H1147H15Landesman-Lazer conditionLeray Schauder degree
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 40 , Issue 4 , 01 December 1997 , pp. 464 - 470
Copyright
Copyright © Canadian Mathematical Society 1997

References

1. Agmon, S., Douglis, A. and Nirenberg, L., Estimates near the boundary for solutions of elliptic partial differential equations satisfying general boundary conditions I. Comm. Pure Appl. Math 12 (1959), 623–727.Google Scholar
2. Berestycki, H. and de Figueiredo, D. G., Double resonance in semilinear elliptic equations. Comm. Partial Differential Equations 6 (1981), 91–120.Google Scholar
3. Gupta, C. P., Perturbations of second order elliptic problems by unbounded nonlinearities. Nonlinear Anal. 6 (1982), 919–933.Google Scholar
4. Hirano, N., Nonlinear perturbations of second order linear elliptic boundary value problems. Houston J. Math. 14 (1988), 105–114.Google Scholar
5. Iannacci, R., Nkashama, M. N. and Ward, J. R. Jr., Nonlinear second order elliptic partial differential equations at resonance. Trans. Amer.Math. Soc. 311 (1989), 711–726.Google Scholar
6. Kannan, R. and Ortega, R., Landesman-Lazer conditions for problems with “one-side unbounded” nonlinearities. Nonlinear Anal. 9 (1985), 1313–1317.Google Scholar
7. Kuo, C.-C., On the solvability of a nonlinear second order elliptic equation at resonance. Proc.Amer.Math. Soc. 24 (1996), 83–87.Google Scholar
8. Landesman, E. M. and Lazer, A. C., Nonlinear perturbations of linear elliptic boundary value problems at resonance. J. Math. Mech. 19 (1970), 609–623.Google Scholar
9. Lloyd, N. G., Degree theory. Cambridge University Press, New York, 1978.Google Scholar
10. McKenna, P. J. and Rauch, J., Strongly nonlinear perturbations of nonnegative boundary value problems with kernel. J. Differential Equations 28 (1978), 253–265.Google Scholar
11. Robinson, S. B. and Landesman, E. M., A general approach to solvability conditions for semilinear elliptic boundary value problems at resonance. Differential Integral Equations 8 (1995), 1555–1569.Google Scholar