Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T18:02:05.525Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Smirnov Class Defined by the Maximal Function

Published online by Cambridge University Press:  20 November 2018

Marek Nawrocki
Marek Nawrocki*
Affiliation:
Faculty of Mathematics and Informatics, A. Mickiewicz University, ul. Matejki 48/49, 60-769 Poznán, Poland, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

H. O. Kim has shown that contrary to the case of 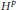${{H}^{p}}$-space, the Smirnov class 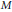$M$ defined by the radial maximal function is essentially smaller than the classical Smirnov class of the disk. In the paper we show that these two classes have the same corresponding locally convex structure, i.e. they have the same dual spaces and the same Fréchet envelopes. We describe a general form of a continuous linear functional on 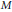$M$ and multiplier from 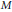$M$ into 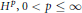${{H}^{p}},\,0\,<\,p\,\le \,\infty $.

Keywords

46E1030A7830A76Smirnov classmaximal radial functionmultipliersdual spaceFréchet envelope
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 45 , Issue 2 , 01 June 2002 , pp. 265 - 271
Copyright
Copyright © Canadian Mathematical Society 2002

References

[D] Duren, P. L., Theory of Hp spaces. Academic Press, New York and London, 1979.Google Scholar
[DRS] Duren, P. L., Romberg, B. W. and Shields, A. L., Linear functionals on Hp with 0 < p < 1. J. Reine Angew. Math. 238 (1969), 238–1969.Google Scholar
[K] Kim, H. O., On an F-algebra of holomorphic functions. Canad. J. Math. (3) 40 (1988), 40–1988.Google Scholar
[N1] Nawrocki, M., The Fréchet envelopes of vector-valued Smirnov classes. Studia Math. 44(1989). 163–177.Google Scholar
[N2] Nawrocki, M., Linear functionals on the Smirnov class of the unit ball in Cn . Ann. Acad. Sci. Fenn. (2) 14 (1990), 14–1990.Google Scholar
[R] Rudin, W., Function Theory in the Unit Ball of Cn . Springer-Verlag, New York, Heidelberg, Berlin, 1980.Google Scholar
[S] Shapiro, J. H., Mackey topologies, reproducing kernels, and diagonal maps on Hardy and Bergman spaces. Duke Math. J. 43 (1976), 43–1976.Google Scholar
[SS] Shapiro, J. H. and Shields, A. L., Unusual topological properties of the Nevanlinna class. Amer. J. Math. 97 (1976), 97–1976.Google Scholar
[ST] Stoll, M., Mean growth and Taylor coefficients of some topological algebras of holomorphic functions. Ann. Polon. Math. 35(1977), pages 141–158.Google Scholar
[Y1] Yanagihara, N., The containing Fréchet space for the class N+ . Duke Math. J. 40 (1973), 40–1973.Google Scholar
[Y2] Yanagihara, N., Multipliers and linear functionals for the class N+ . Trans. Amer. Math. Soc. 180 (1973), 180–1973.Google Scholar
[Y3] Yanagihara, N., Mean growth and Taylor coefficients of some classes of functions. Ann. Polon. Math. 30 (1974), 30–1974.Google Scholar