On the Smallest and Largest Zeros of Müntz-Legendre Polynomials

Abstract

Müntz-Legendre polynomials 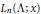${{L}_{n}}\left( \Lambda ;\,x \right)$ associated with a sequence 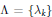$\Lambda \,=\,\left\{ {{\lambda }_{k}} \right\}$ are obtained by orthogonalizing the system 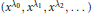$\left( {{x}^{{{\lambda }_{0}}}},{{x}^{{{\lambda }_{1}}}},{{x}^{{{\lambda }_{2}}}},... \right)$ in 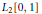${{L}_{2}}\left[ 0,1 \right]$ with respect to the Legendre weight. If the 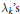${{\lambda }_{k}}\text{ }\!\!'\!\!\text{ s}$ are distinct, it is well known that 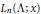${{L}_{n}}\left( \Lambda ;\,x \right)$ has exactly $n$ zeros 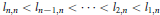${{l}_{n,n}}\,<\,{{l}_{n-1,n}}\,<\,\cdot \cdot \cdot \,<\,{{l}_{2,n}}\,<\,{{l}_{1,n}}$ on 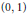$\left( 0,1 \right)$.

First we prove the following global bound for the smallest zero,

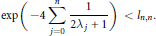$$\exp \left( -4\sum\limits_{j=0}^{n}{\frac{1}{2\text{ }\!\!\lambda\!\!\text{ j}\,\text{+}\,\text{1}}} \right)\,<\,{{l}_{n,n}}.$$

An important consequence is that if the associated Müntz space is non-dense in 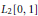${{L}_{2}}\left[ 0,1 \right]$, then

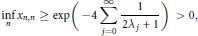$$\underset{n}{\mathop{\inf }}\,\,{{x}_{n,n}}\,\ge \,\exp \,\left( -4\,\sum\limits_{j=0}^{\infty }{\frac{1}{2{{\text{ }\!\!\lambda\!\!\text{ }}_{j}}\,+\,1}} \right)\,>\,0,$$

so the elements 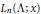${{L}_{n}}\left( \Lambda ;\,x \right)$ have no zeros close to 0.

Furthermore, we determine the asymptotic behavior of the largest zeros; for $k$ fixed,

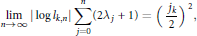$$\underset{n\to \infty }{\mathop{\lim }}\,\,\left| \log \,{{l}_{k,n}} \right|\,\sum\limits_{j=0}^{n}{\left( 2{{\text{ }\!\!\lambda\!\!\text{ }}_{j}}\,+\,1 \right)}\,=\,{{\left( \frac{jk}{2} \right)}^{2}},$$

where 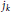${{j}_{k}}$ denotes the $k$-th zero of the Bessel function 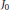${{J}_{0}}.$