Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Paulsen, Vern I.
2006.
Equivariant maps and bimodule projections.
Journal of Functional Analysis,
Vol. 240,
Issue. 2,
p.
495.
Juschenko, K.
Levene, R.H.
Todorov, I.G.
and
Turowska, L.
2009.
Compactness properties of operator multipliers.
Journal of Functional Analysis,
Vol. 256,
Issue. 11,
p.
3772.
Forrest, Brian E.
and
Runde, Volker
2011.
Norm One Idempotent cb-Multipliers with Applications to the Fourier Algebra in the cb-Multiplier Norm.
Canadian Mathematical Bulletin,
Vol. 54,
Issue. 4,
p.
654.
Eleftherakis, G.K.
and
Todorov, I.G.
2012.
Ranges of bimodule projections and reflexivity.
Journal of Functional Analysis,
Vol. 262,
Issue. 11,
p.
4891.
Steen, N.M.
Todorov, I.G.
and
Turowska, L.
2014.
Local operator multipliers and positivity.
Journal of Functional Analysis,
Vol. 267,
Issue. 1,
p.
80.
Anoussis, M.
Katavolos, A.
and
Todorov, I.G.
2014.
Ideals ofA(G)and bimodules over maximal abelian selfadjoint algebras.
Journal of Functional Analysis,
Vol. 266,
Issue. 11,
p.
6473.
Shulman, V.S.
Todorov, I.G.
and
Turowska, L.
2015.
Sets of multiplicity and closable multipliers on group algebras.
Journal of Functional Analysis,
Vol. 268,
Issue. 6,
p.
1454.
Eleftherakis, G.
and
Todorov, I.
2015.
Operator synthesis and tensor products.
Transactions of the American Mathematical Society,
Vol. 368,
Issue. 8,
p.
5271.
ANOUSSIS, M.
KATAVOLOS, A.
and
TODOROV, I. G.
2016.
Ideals of the Fourier algebra, supports and harmonic operators.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 161,
Issue. 2,
p.
223.
Eleftherakis, G. K.
Levene, R. H.
and
Todorov, I. G.
2016.
Schur idempotents and hyperreflexivity.
Israel Journal of Mathematics,
Vol. 215,
Issue. 1,
p.
317.
Levene, R. H.
Spronk, N.
Todorov, I. G.
and
Turowska, L.
2017.
Schur Multipliers of Cartan Pairs.
Proceedings of the Edinburgh Mathematical Society,
Vol. 60,
Issue. 2,
p.
413.
McKee, A.
Todorov, I.G.
and
Turowska, L.
2018.
Herz–Schur multipliers of dynamical systems.
Advances in Mathematics,
Vol. 331,
Issue. ,
p.
387.
Pluta, Robert
and
Russo, Bernard
2018.
Projections on von Neumann algebras as limits of elementary operators.
Linear Algebra and its Applications,
Vol. 557,
Issue. ,
p.
188.
McKee, Andrew
2021.
Multipliers and Duality for Group Actions.
Journal of Fourier Analysis and Applications,
Vol. 27,
Issue. 6,
Hambardzumyan, Lianna
Hatami, Hamed
and
Hatami, Pooya
2023.
Dimension-free bounds and structural results in communication complexity.
Israel Journal of Mathematics,
Vol. 253,
Issue. 2,
p.
555.
Exel, Ruy
Pitts, David R.
and
Zarikian, Vrej
2023.
Exotic ideals in free transformation group C∗$\mathbf {C}^*$‐algebras.
Bulletin of the London Mathematical Society,
Vol. 55,
Issue. 3,
p.
1489.
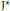 ${{\text{J}}^{*}}$-algebras. We prove that if
${{\text{J}}^{*}}$-algebras. We prove that if  $P$ is a normal bimodule idempotent and
$P$ is a normal bimodule idempotent and 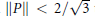 $\left\| P \right\|\,<\,2/\sqrt{3}$ then
$\left\| P \right\|\,<\,2/\sqrt{3}$ then  $P$ is a contraction. We finish with some attempts at extending the symbol calculus to non-normal maps.
$P$ is a contraction. We finish with some attempts at extending the symbol calculus to non-normal maps.

