Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T15:09:29.904Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Projective Cover of the Stone-Čech Compactification of a Completely Regular Hausdorff Space

Published online by Cambridge University Press:  20 November 2018

Young Lim Park
Young Lim Park*
Affiliation:
Laurentian University, Sudbury, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The main object of this paper is to give an explicit object in the study of projective covers in the category of compact Hausdorff spaces and continuous maps studied in [2] and [5]. 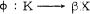be a projective cover of the Stone-Čech compactification βX of a completely regular Hausdorff space X. Here, it will be shown that the maximal ideal space endowed with the Stone topology of the maximal ring of quotients of the ring C(X) of all real valued continuous functions on X is homeomorphic to K.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 12 , Issue 3 , June 1969 , pp. 327 - 331
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Banaschewski, B., Maximal rings of quotients of semi-simple commutative rings. Arch. Math. 16 (1965) 414–420.Google Scholar
2. Banaschewski, B., Projective covers in certain categories of topological spaces. (Unpublished manuscript.)Google Scholar
3. Fine, N., Gillman, L. and Lambek, J., Rings of quotients of rings of functions. (McGill Univ. Press, Montreal, 1965.)Google Scholar
4. Gillman, L. and Jerison, M., Rings of continuous functions. (Princeton, 1960.)Google Scholar
5. Gleason, A.M., Projective topological spaces. III. J. Math. 2 (1958) 482–489.Google Scholar