No CrossRef data available.
Article contents
On the Notion of Visibility of Torsors
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 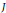 $J$ be an abelian variety and
$J$ be an abelian variety and 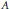 $A$ be an abelian subvariety of
$A$ be an abelian subvariety of 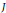 $J$ , both defined over
$J$ , both defined over 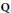 $Q$. Let
$Q$. Let 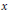 $x$ be an element of
$x$ be an element of 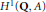 ${{H}^{1}}\left( Q,\,A \right)$. Then there are at least two definitions of
${{H}^{1}}\left( Q,\,A \right)$. Then there are at least two definitions of 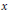 $x$ being visible in
$x$ being visible in 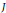 $J$: one asks that the torsor corresponding to
$J$: one asks that the torsor corresponding to 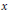 $x$ be isomorphic over
$x$ be isomorphic over 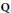 $Q$ to a subvariety of
$Q$ to a subvariety of 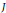 $J$, and the other asks that
$J$, and the other asks that 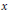 $x$ be in the kernel of the natural map
$x$ be in the kernel of the natural map 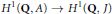 $
{{H}^{1}}\left( Q,\,A \right)\,\to \,{{H}^{1}}\left( \text{Q},\,J \right)$. In this article, we clarify the relation between the two definitions.
$
{{H}^{1}}\left( Q,\,A \right)\,\to \,{{H}^{1}}\left( \text{Q},\,J \right)$. In this article, we clarify the relation between the two definitions.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2013


