Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-12-03T19:35:23.365Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Non-Existence of Conjugate Points

Published online by Cambridge University Press:  20 November 2018

G. J. Butler ,
L. H. Erbe  and
R. M. Mathsen
G. J. Butler
Affiliation:
University of Alberta, Edmonton, Alberta
L. H. Erbe
Affiliation:
University of Alberta, Edmonton, Alberta
R. M. Mathsen
Affiliation:
University of Alberta, Edmonton, Alberta
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we consider the types of pairs of multiple zeros which a solution to the differential equation

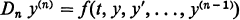
can possess on an interval I of the real line. The results obtained generalize those in [2] and (for n = 3) in [3].

I. Let f satisfy the condition

1.1

for all t ∊ I, u0 ≠ 0, and all u1, … un-1.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 13 , Issue 1 , March 1970 , pp. 31 - 37
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Bebernes, J. W., A subfunction approach to a boundary value problem for ordinary differential equations, Pacific J. Math. 13, No. 4 (1963), 1053-1066.Google Scholar
2. Eliason, S. B., Nonperiodicity of solutions of an Nth-order equation, Amer. Math. Monthly (to appear).Google Scholar
3. Mathsen, R. M., A note on solutions of third-order ordinary differential equations, SIAM Rev. (to appear).Google Scholar
4. Sherman, T. L., On solutions of Nth-order linear differential equations with N zeros, Bull. Am. Math. Soc. 74, No. 5 (1968), 923-925.Google Scholar
5. Sherman, T. L., Conjugate points and simple zeros for ordinary linear differential equations (submitted for publication).Google Scholar