Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2025-01-01T05:03:18.830Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Non-Existence of Certain Euler Products

Published online by Cambridge University Press:  20 November 2018

M. V. Subbarao
M. V. Subbarao*
Affiliation:
Department of Mathematics University of Alberta Edmonton, Alberta, Canada T6G 2G1
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a paper with the above title, T. M. Apostol and S. Chowla [1] proved the following result:

Theorem 1.For relatively prime integers h and k, l ≤ h ≤ k, the series

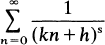
does not admit of an Euler product decomposition, that is, an identity of the form

1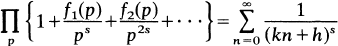

except when h = k = l; fc = 1, fc = 2. The series on the right is extended over all primes p and is assumed to be absolutely convergent forR(s)>1.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 23 , Issue 3 , 01 September 1980 , pp. 371 - 372
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Apostol, T.M. and Chowla, S., On the Non-Existence of Certain Euler Products, Det Kongelige Norske Videnskabers Selskab Forhandlinger Vol. 32 (1959), No. II, 65-67.Google Scholar
2. James, R.D. and Ivan, Niven, Unique Factorization in Multiplicative Systems, Proc. Amer. Math. Soc. 5 (1954); 834-838, MR16 336.Google Scholar