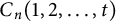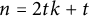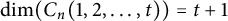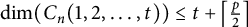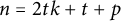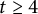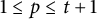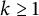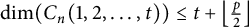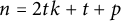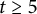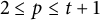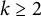1 Introduction
Let
![]() $G=(V(G),E(G))$
be a simple undirected connected graph. The distance
$G=(V(G),E(G))$
be a simple undirected connected graph. The distance
![]() $d(u,v)$
between two vertices u and v in G is the length of a shortest path between these two vertices. For an ordered set
$d(u,v)$
between two vertices u and v in G is the length of a shortest path between these two vertices. For an ordered set
![]() $W=\{w_1,\ldots ,w_k\}$
of k distinct vertices of G, we refer to the k-tuple
$W=\{w_1,\ldots ,w_k\}$
of k distinct vertices of G, we refer to the k-tuple
![]() $r(v|W)=(d(v,w_1),d(v,w_2),\ldots ,d(v,w_k))$
as the metric representation of a vertex v with respect to W. The set W is called a resolving set of G if
$r(v|W)=(d(v,w_1),d(v,w_2),\ldots ,d(v,w_k))$
as the metric representation of a vertex v with respect to W. The set W is called a resolving set of G if
![]() $r(u|W)=r(v|W)$
implies that
$r(u|W)=r(v|W)$
implies that
![]() $u=v$
for all
$u=v$
for all
![]() $u,v\in V(G)$
. A resolving set containing a minimum number of vertices is called a metric basis of G, and its cardinality the metric dimension of G, denoted by
$u,v\in V(G)$
. A resolving set containing a minimum number of vertices is called a metric basis of G, and its cardinality the metric dimension of G, denoted by
![]() $\mathrm {dim}(G)$
.
$\mathrm {dim}(G)$
.
Motivated by the problem of uniquely determining the location of an intruder in a network, Slater introduced the notion of metric dimension of a graph in [Reference Slater9], where the resolving sets were referred to as locating sets. Harary and Melter also introduced the idea of the metric dimension of a graph in [Reference Harary and Melter5]. It was proved that the metric dimension is an NP-hard graph invariant [Reference Khuller, Raghavachari and Rosenfeld8] and has been widely investigated in the last 55 years and it also has applications in many diverse areas [Reference Johnson6, Reference Johnson, Carbó-Dorca and Mezey7].
This note is devoted to the study of the metric dimension of circulant graphs. Let n, t, and
![]() $a_1,a_2,\ldots ,a_t$
be positive integers so that
$a_1,a_2,\ldots ,a_t$
be positive integers so that
![]() $1\leq a_1<a_2<\dots <a_t\leq \left \lfloor \frac {n}{2}\right \rfloor $
. The circulant graph
$1\leq a_1<a_2<\dots <a_t\leq \left \lfloor \frac {n}{2}\right \rfloor $
. The circulant graph
![]() $C_n(a_1,a_2,\ldots ,a_t)$
consists of a vertex set
$C_n(a_1,a_2,\ldots ,a_t)$
consists of a vertex set
![]() $\{v_0,v_1,\ldots ,v_{n-1}\}$
and an edge set
$\{v_0,v_1,\ldots ,v_{n-1}\}$
and an edge set
![]() $\{v_iv_{i+a_j}:0\leq i\leq n-1,1\leq j\leq t\}$
, where the indices are taken modulo n. The numbers
$\{v_iv_{i+a_j}:0\leq i\leq n-1,1\leq j\leq t\}$
, where the indices are taken modulo n. The numbers
![]() $a_1,a_2,\ldots ,a_t$
are called generators. We restrict our attention to special kinds of circulant graphs, i.e., the circulant graphs
$a_1,a_2,\ldots ,a_t$
are called generators. We restrict our attention to special kinds of circulant graphs, i.e., the circulant graphs
![]() $C_n(1,2,\ldots ,t)$
with consecutive generators. In [Reference Borchert and Gosselin1], Borchert and Gosselin studied the metric dimension of
$C_n(1,2,\ldots ,t)$
with consecutive generators. In [Reference Borchert and Gosselin1], Borchert and Gosselin studied the metric dimension of
![]() $C_n(1,2)$
and
$C_n(1,2)$
and
![]() $C_n(1,2,3)$
, and obtained that for
$C_n(1,2,3)$
, and obtained that for
![]() $n\geq 6$
,
$n\geq 6$
,
 $$ \begin{align*} \dim(C_n(1,2))=\left\{ \begin{aligned} &4,\quad & \text{for}\,\, n\equiv1 \,\,\text{mod}\,\, 4, \\ &3,\quad & \text{otherwise,}\,\, \end{aligned} \right. \end{align*} $$
$$ \begin{align*} \dim(C_n(1,2))=\left\{ \begin{aligned} &4,\quad & \text{for}\,\, n\equiv1 \,\,\text{mod}\,\, 4, \\ &3,\quad & \text{otherwise,}\,\, \end{aligned} \right. \end{align*} $$
and that for
![]() $n\geq 8$
,
$n\geq 8$
,
 $$ \begin{align*} \dim(C_n(1,2,3))=\left\{ \begin{aligned} &5,\quad & \text{for}\,\, n\equiv1 \,\,\text{mod}\,\, 6, \\ &4,\quad & \text{otherwise.}\,\, \end{aligned} \right. \end{align*} $$
$$ \begin{align*} \dim(C_n(1,2,3))=\left\{ \begin{aligned} &5,\quad & \text{for}\,\, n\equiv1 \,\,\text{mod}\,\, 6, \\ &4,\quad & \text{otherwise.}\,\, \end{aligned} \right. \end{align*} $$
In [Reference Grigorious, Kalinowski, Ryan and Stephen3, Reference Vetrík11], the authors studied the metric dimension of
![]() $C_n(1,2,3,4)$
, and obtained that for
$C_n(1,2,3,4)$
, and obtained that for
![]() $n\geq 20$
,
$n\geq 20$
,
 $$ \begin{align*} \dim(C_n(1,2,3,4))=\left\{ \begin{aligned} &6,\quad & \text{for}\,\, n\equiv0,1,7 \,\,\text{mod}\,\, 8, \\ &5,\quad & \text{for}\,\, n\equiv2,3,5,6 \,\,\text{mod}\,\, 8, \\ &4,\quad & \text{for}\,\, n\equiv4 \,\,\text{mod}\,\, 8. \end{aligned} \right. \end{align*} $$
$$ \begin{align*} \dim(C_n(1,2,3,4))=\left\{ \begin{aligned} &6,\quad & \text{for}\,\, n\equiv0,1,7 \,\,\text{mod}\,\, 8, \\ &5,\quad & \text{for}\,\, n\equiv2,3,5,6 \,\,\text{mod}\,\, 8, \\ &4,\quad & \text{for}\,\, n\equiv4 \,\,\text{mod}\,\, 8. \end{aligned} \right. \end{align*} $$
For the results concerning
![]() $\dim (C_n(1,2,\ldots ,t))$
with arbitrary integers
$\dim (C_n(1,2,\ldots ,t))$
with arbitrary integers
![]() $t\geq 5$
, the reader may refer to [Reference Chau and Gosselin2, Reference Grigorious, Manuel, Miller, Rajan and Stephen4, Reference Vetrík10, Reference Vetrík12].
$t\geq 5$
, the reader may refer to [Reference Chau and Gosselin2, Reference Grigorious, Manuel, Miller, Rajan and Stephen4, Reference Vetrík10, Reference Vetrík12].
We shall assume throughout this note that
![]() $n=2tk+r$
, where
$n=2tk+r$
, where
![]() $t\geq 4$
,
$t\geq 4$
,
![]() $k\geq 2$
, and
$k\geq 2$
, and
![]() $2\leq r\leq 2t+1$
. When
$2\leq r\leq 2t+1$
. When
![]() $t\leq r\leq 2t+1$
, we may also assume
$t\leq r\leq 2t+1$
, we may also assume
![]() $n=2tk+t+p$
, where
$n=2tk+t+p$
, where
![]() $0\leq p\leq t+1$
. It is known that the distance between two vertices
$0\leq p\leq t+1$
. It is known that the distance between two vertices
![]() $v_i$
and
$v_i$
and
![]() $v_j$
in
$v_j$
in
![]() $C_n(1,2,\ldots ,t)$
is
$C_n(1,2,\ldots ,t)$
is
 $$ \begin{align} d(v_i,v_j)=\min\left\{\left\lceil\frac{|i-j|}{t}\right\rceil,\left\lceil\frac{n-|i-j|}{t}\right\rceil\right\}, \end{align} $$
$$ \begin{align} d(v_i,v_j)=\min\left\{\left\lceil\frac{|i-j|}{t}\right\rceil,\left\lceil\frac{n-|i-j|}{t}\right\rceil\right\}, \end{align} $$
and that the diameter of
![]() $C_n(1,2,\ldots ,t)$
is
$C_n(1,2,\ldots ,t)$
is
![]() $d:= k+1$
.
$d:= k+1$
.
Here, we set forth our notation and terminology. Let W and V be subsets of vertices in
![]() $G=C_n(1,2,\ldots ,t)$
, where V consists of at least two vertices. A vertex w is said to resolve a pair of vertices u and v if
$G=C_n(1,2,\ldots ,t)$
, where V consists of at least two vertices. A vertex w is said to resolve a pair of vertices u and v if
![]() $d(u,w)\neq d(v,w)$
. W is said to distinguish V if for any pair of distinct vertices u and v in V, there exists a vertex in W which can resolve u and v. It is easy to see that if W can distinguish
$d(u,w)\neq d(v,w)$
. W is said to distinguish V if for any pair of distinct vertices u and v in V, there exists a vertex in W which can resolve u and v. It is easy to see that if W can distinguish
![]() $V(G)$
, then it is a resolving set of G. Vertices
$V(G)$
, then it is a resolving set of G. Vertices
![]() $v_{i+1},v_{i+2},\ldots ,v_{i+s}$
with consecutive indices are called the consecutive vertices. The outer cycle of the circulant graph is a spanning subgraph of G in which the vertex
$v_{i+1},v_{i+2},\ldots ,v_{i+s}$
with consecutive indices are called the consecutive vertices. The outer cycle of the circulant graph is a spanning subgraph of G in which the vertex
![]() $v_i$
is adjacent to exactly the vertices
$v_i$
is adjacent to exactly the vertices
![]() $v_{i+1}$
and
$v_{i+1}$
and
![]() $v_{i-1}$
. When
$v_{i-1}$
. When
![]() $r=2$
, the unique vertex that has distance
$r=2$
, the unique vertex that has distance
![]() $k+1$
from w will be called the opposite vertex of w, and is denoted by
$k+1$
from w will be called the opposite vertex of w, and is denoted by
![]() $w^{'}$
, and we can then define
$w^{'}$
, and we can then define
![]() $W^{'}:=\{w^{'}:w\in W\}$
for the vertex set W.
$W^{'}:=\{w^{'}:w\in W\}$
for the vertex set W.
2 Lower bounds
This section deals with the lower bounds for
![]() $\dim (C_n(1,2,\ldots ,t))$
. In [Reference Chau and Gosselin2, Reference Vetrík10], the authors have shown that when
$\dim (C_n(1,2,\ldots ,t))$
. In [Reference Chau and Gosselin2, Reference Vetrík10], the authors have shown that when
![]() $3\leq r\leq t$
and n is sufficiently large,
$3\leq r\leq t$
and n is sufficiently large,
![]() $\dim (C_n(1,2,\ldots ,t))$
has a lower bound of t.
$\dim (C_n(1,2,\ldots ,t))$
has a lower bound of t.
Theorem 2.1 ([Reference Vetrík10, Theorem 2.3]) Let
![]() $n=2tk+r$
where
$n=2tk+r$
where
![]() $3\leq r\leq t$
, and
$3\leq r\leq t$
, and
![]() $n\geq t^2+1$
. Then
$n\geq t^2+1$
. Then
![]() $\dim (C_n(1,2,\ldots ,t))\geq t$
.
$\dim (C_n(1,2,\ldots ,t))\geq t$
.
Theorem 2.3 improves their result. We begin with the following lemma.
Lemma 2.2 Suppose that
![]() $r=t$
, and that
$r=t$
, and that
![]() $2\leq x\leq t$
. If a vertex set W can distinguish x consecutive vertices, then the cardinality of W is at least
$2\leq x\leq t$
. If a vertex set W can distinguish x consecutive vertices, then the cardinality of W is at least
![]() $x-1$
.
$x-1$
.
Proof Without loss of generality, assume that W can distinguish
![]() $V{\kern-1.5pt}={\kern-1pt}\{v_1,v_2,\ldots ,v_x\}$
. Let
$V{\kern-1.5pt}={\kern-1pt}\{v_1,v_2,\ldots ,v_x\}$
. Let
![]() $W_1$
be the intersection of W and V, and p the cardinality of
$W_1$
be the intersection of W and V, and p the cardinality of
![]() $W_1$
. We can assume
$W_1$
. We can assume
![]() $p\leq x-2$
, and then assume
$p\leq x-2$
, and then assume
![]() $V\backslash W_1=\{v_{i_1},\ldots ,v_{i_{x-p}}\}$
, where
$V\backslash W_1=\{v_{i_1},\ldots ,v_{i_{x-p}}\}$
, where
![]() $i_1<\cdots <i_{x-p}$
. It follows that
$i_1<\cdots <i_{x-p}$
. It follows that
![]() $W\backslash W_1$
can distinguish
$W\backslash W_1$
can distinguish
![]() $x-p-1$
pairs of vertices
$x-p-1$
pairs of vertices
![]() $(v_{i_1},v_{i_2}),\ldots ,(v_{i_{x-p-1}},v_{i_{x-p}})$
. Suppose
$(v_{i_1},v_{i_2}),\ldots ,(v_{i_{x-p-1}},v_{i_{x-p}})$
. Suppose
![]() $w_j\in W\backslash W_1$
can resolve
$w_j\in W\backslash W_1$
can resolve
![]() $(v_{i_j},v_{i_{j+1}})$
for each such j, then it can resolve two consecutive vertices in the
$(v_{i_j},v_{i_{j+1}})$
for each such j, then it can resolve two consecutive vertices in the
![]() $v_{i_j}-v_{i_{j+1}}$
path of the outer cycle, say
$v_{i_j}-v_{i_{j+1}}$
path of the outer cycle, say
![]() $v_{i_j^{'}}$
and
$v_{i_j^{'}}$
and
![]() $v_{i_j^{'}+1}$
. Since
$v_{i_j^{'}+1}$
. Since
![]() $r=t$
, and since the distance between
$r=t$
, and since the distance between
![]() $v_{i_1}$
and
$v_{i_1}$
and
![]() $v_{i_j^{'}}$
on the outer cycle is no more than
$v_{i_j^{'}}$
on the outer cycle is no more than
![]() $t-2$
, it follows from equation (1.1) that
$t-2$
, it follows from equation (1.1) that
![]() $d(v_{i_1},w_j)=d(v_{i_1+1},w_j)=\cdots =d(v_{i_j^{'}},w_j)$
, and thus none of the pairs
$d(v_{i_1},w_j)=d(v_{i_1+1},w_j)=\cdots =d(v_{i_j^{'}},w_j)$
, and thus none of the pairs
![]() $(v_{i_1},v_{i_2}),\ldots ,(v_{i_{j-1}},v_{i_{j}})$
can be resolved by
$(v_{i_1},v_{i_2}),\ldots ,(v_{i_{j-1}},v_{i_{j}})$
can be resolved by
![]() $w_j$
. A similar argument shows that none of the pairs
$w_j$
. A similar argument shows that none of the pairs
![]() $(v_{i_{j+1}},v_{i_{j+2}}),\ldots ,(v_{i_{x-p-1}},v_{i_{x-p}})$
can be resolved by
$(v_{i_{j+1}},v_{i_{j+2}}),\ldots ,(v_{i_{x-p-1}},v_{i_{x-p}})$
can be resolved by
![]() $w_j$
. Therefore, any vertex in
$w_j$
. Therefore, any vertex in
![]() $W\backslash W_1$
resolving one of the pairs
$W\backslash W_1$
resolving one of the pairs
![]() $(v_{i_1},v_{i_2}),\ldots ,(v_{i_{x-p-1}},v_{i_{x-p}})$
cannot resolve the other, implying that
$(v_{i_1},v_{i_2}),\ldots ,(v_{i_{x-p-1}},v_{i_{x-p}})$
cannot resolve the other, implying that
![]() $W\backslash W_1$
consists of at least
$W\backslash W_1$
consists of at least
![]() $x-p-1$
vertices, and so
$x-p-1$
vertices, and so
![]() $\sharp (W)\geq x-1$
.
$\sharp (W)\geq x-1$
.
Theorem 2.3 Let
![]() $n=2tk+t$
where t is odd. Then
$n=2tk+t$
where t is odd. Then
![]() $\dim (C_n(1,2,\ldots ,t))\geq t+1$
.
$\dim (C_n(1,2,\ldots ,t))\geq t+1$
.
Proof Let W be a resolving set of the graph
![]() $C_n(1,2,\ldots ,t)$
. Suppose on the contrary that
$C_n(1,2,\ldots ,t)$
. Suppose on the contrary that
![]() $\sharp (W)=t$
. We can assume
$\sharp (W)=t$
. We can assume
![]() $v_0\in W$
.
$v_0\in W$
.
Let us first show that
![]() $W\cap \{v_{i-tk},v_{i+tk}\}\neq \emptyset $
holds for each vertex
$W\cap \{v_{i-tk},v_{i+tk}\}\neq \emptyset $
holds for each vertex
![]() $v_i\in W$
. Suppose on the contrary that there exists a vertex
$v_i\in W$
. Suppose on the contrary that there exists a vertex
![]() $v_j\in W$
with
$v_j\in W$
with
![]() $W\cap \{v_{j-tk},v_{j+tk}\}=\emptyset $
, since the circulant graph
$W\cap \{v_{j-tk},v_{j+tk}\}=\emptyset $
, since the circulant graph
![]() $C_n(1,2,\ldots ,t)$
is vertex-transitive, and we may take
$C_n(1,2,\ldots ,t)$
is vertex-transitive, and we may take
![]() $j=0$
. Let
$j=0$
. Let
![]() $p\geq 0$
be such that
$p\geq 0$
be such that
![]() $v_{n-0},v_{n-1},\ldots ,v_{n-p}$
all belong to W while
$v_{n-0},v_{n-1},\ldots ,v_{n-p}$
all belong to W while
![]() $v_{n-p-1}\notin W$
, and let
$v_{n-p-1}\notin W$
, and let
![]() $q\geq 0$
be such that
$q\geq 0$
be such that
![]() $v_{0},v_{1},\ldots ,v_{q}$
all belong to W while
$v_{0},v_{1},\ldots ,v_{q}$
all belong to W while
![]() $v_{q+1}\notin W$
. It is easy to see that
$v_{q+1}\notin W$
. It is easy to see that
![]() $p+q\leq t-1$
. Set
$p+q\leq t-1$
. Set
![]() $W_1=\{v_{n-p},v_{n-p+1},\ldots ,v_{q}\}$
. Then there is a vertex
$W_1=\{v_{n-p},v_{n-p+1},\ldots ,v_{q}\}$
. Then there is a vertex
![]() $w\in W\backslash {W_1}$
that resolves
$w\in W\backslash {W_1}$
that resolves
![]() $v_{n-p-1}$
and
$v_{n-p-1}$
and
![]() $v_{q+1}$
. If
$v_{q+1}$
. If
![]() $p+q=t-1$
, then W consists of at least
$p+q=t-1$
, then W consists of at least
![]() $t+1$
vertices, leading to the contradiction. Suppose now that
$t+1$
vertices, leading to the contradiction. Suppose now that
![]() $p+q\leq t-2$
. One can verify that there are two consecutive vertices
$p+q\leq t-2$
. One can verify that there are two consecutive vertices
![]() $v_i$
and
$v_i$
and
![]() $v_{i+1}$
in the
$v_{i+1}$
in the
![]() $v_{n-p-1}-v_{q+1}$
path of the outer cycle, which can be resolved by w. By symmetry, we can assume
$v_{n-p-1}-v_{q+1}$
path of the outer cycle, which can be resolved by w. By symmetry, we can assume
![]() $n-t+1\leq i\leq n-1$
.
$n-t+1\leq i\leq n-1$
.
First, consider the case
![]() $n-t+1\leq i\leq n-2$
. Note that
$n-t+1\leq i\leq n-2$
. Note that
![]() $\{v_{i+1},v_{i+2},\ldots ,v_n\}\subset W_1$
, and that
$\{v_{i+1},v_{i+2},\ldots ,v_n\}\subset W_1$
, and that
![]() $W\backslash (\{v_{i+1},v_{i+2},\ldots ,v_n\}\cup \{w\})$
can distinguish
$W\backslash (\{v_{i+1},v_{i+2},\ldots ,v_n\}\cup \{w\})$
can distinguish
![]() $\{v_{n-t},v_{n-t+1},\ldots ,v_{i}\}$
, which consists of
$\{v_{n-t},v_{n-t+1},\ldots ,v_{i}\}$
, which consists of
![]() $i+t+1-n$
vertices. It follows from Lemma 2.2 that
$i+t+1-n$
vertices. It follows from Lemma 2.2 that
![]() $W\backslash (\{v_{i+1},v_{i+2},\ldots ,v_n\}\cup \{w\})$
has at least
$W\backslash (\{v_{i+1},v_{i+2},\ldots ,v_n\}\cup \{w\})$
has at least
![]() $i+t-n$
vertices, and therefore
$i+t-n$
vertices, and therefore
![]() $\sharp (W)\geq t+1$
, a contradiction.
$\sharp (W)\geq t+1$
, a contradiction.
Next, consider the case where
![]() $i=n-1$
. Since
$i=n-1$
. Since
![]() $w\notin \{v_{n-1},v_0,v_{kt}\}$
, and since
$w\notin \{v_{n-1},v_0,v_{kt}\}$
, and since
![]() $r=t$
, it follows from equation (1.1) that vertices
$r=t$
, it follows from equation (1.1) that vertices
![]() $v_{n-t},v_{n-t+1},\ldots ,v_{n-1}$
have equal distance to w. Hence,
$v_{n-t},v_{n-t+1},\ldots ,v_{n-1}$
have equal distance to w. Hence,
![]() $W\backslash \{v_0,w\}$
can distinguish
$W\backslash \{v_0,w\}$
can distinguish
![]() $\{v_{n-t},v_{n-t+1},\ldots ,v_{n-1}\}$
, and applying Lemma 2.2,
$\{v_{n-t},v_{n-t+1},\ldots ,v_{n-1}\}$
, and applying Lemma 2.2,
![]() $W\backslash \{v_0,w\}$
has at least
$W\backslash \{v_0,w\}$
has at least
![]() $t-1$
vertices, and therefore W consists of at least
$t-1$
vertices, and therefore W consists of at least
![]() $t+1$
vertices, which is a contradiction.
$t+1$
vertices, which is a contradiction.
We have already verified that
![]() $W\cap \{v_{i-tk},v_{i+tk}\}\neq \emptyset $
holds for each vertex
$W\cap \{v_{i-tk},v_{i+tk}\}\neq \emptyset $
holds for each vertex
![]() $v_i\in W$
. We now claim that
$v_i\in W$
. We now claim that
![]() $|W\cap \{v_{i-tk},v_{i+tk}\}|=1$
holds for each vertex
$|W\cap \{v_{i-tk},v_{i+tk}\}|=1$
holds for each vertex
![]() $v_i\in W$
. Suppose on the contrary that there is a vertex
$v_i\in W$
. Suppose on the contrary that there is a vertex
![]() $v_j\in W$
with
$v_j\in W$
with
![]() $\{v_{j-tk},v_{j+tk}\}\subset W$
, and we may also take
$\{v_{j-tk},v_{j+tk}\}\subset W$
, and we may also take
![]() $j=0$
. Then
$j=0$
. Then
![]() $W\backslash \{v_0,v_{kt},v_{n-kt}\}$
can distinguish
$W\backslash \{v_0,v_{kt},v_{n-kt}\}$
can distinguish
![]() $\{v_{kt+1},v_{kt+2},\ldots ,v_{kt+t-1}\}$
, and applying Lemma 2.2,
$\{v_{kt+1},v_{kt+2},\ldots ,v_{kt+t-1}\}$
, and applying Lemma 2.2,
![]() $W\backslash \{v_0,v_{kt},v_{n-kt}\}$
consists of at least
$W\backslash \{v_0,v_{kt},v_{n-kt}\}$
consists of at least
![]() $t-2$
vertices, and so
$t-2$
vertices, and so
![]() $\sharp (W)\geq t+1$
, a contradiction.
$\sharp (W)\geq t+1$
, a contradiction.
In conclusion, for each vertex
![]() $w\in W$
, there exists exactly one vertex, say
$w\in W$
, there exists exactly one vertex, say
![]() $w_1$
, in W such that
$w_1$
, in W such that
![]() $w_1$
has distance
$w_1$
has distance
![]() $kt$
from w on the outer cycle, and we say
$kt$
from w on the outer cycle, and we say
![]() $\{w,w_1\}$
form a “pair” in W. It is easy to see that these “pairs” in W are pairwise disjoint. Hence, the cardinality of W is even, which contradicts the assumption that
$\{w,w_1\}$
form a “pair” in W. It is easy to see that these “pairs” in W are pairwise disjoint. Hence, the cardinality of W is even, which contradicts the assumption that
![]() $\sharp (W)=t$
is odd.
$\sharp (W)=t$
is odd.
In what follows, we shall discuss the case where
![]() $r\in \{2\}\cup \{t+1,t+2,\ldots ,2t+1\}$
. The following lemma will be needed in the sequel.
$r\in \{2\}\cup \{t+1,t+2,\ldots ,2t+1\}$
. The following lemma will be needed in the sequel.
Lemma 2.4 Suppose that
![]() $r\in \{2\}\cup \{t+1,t+2,\ldots ,2t+1\}$
and that
$r\in \{2\}\cup \{t+1,t+2,\ldots ,2t+1\}$
and that
![]() $2\leq x\leq t$
. If a vertex set W can distinguish x vertices which come from a clique of
$2\leq x\leq t$
. If a vertex set W can distinguish x vertices which come from a clique of
![]() $x+1$
consecutive vertices, then the cardinality of W is at least
$x+1$
consecutive vertices, then the cardinality of W is at least
![]() $x-1$
.
$x-1$
.
Proof Suppose that
![]() $v_{i_1},\ldots ,v_{i_x}$
come from a clique of
$v_{i_1},\ldots ,v_{i_x}$
come from a clique of
![]() $x+1$
consecutive vertices, where
$x+1$
consecutive vertices, where
![]() $i_1<i_2<\cdots <i_x$
, and suppose that W can distinguish them.
$i_1<i_2<\cdots <i_x$
, and suppose that W can distinguish them.
We first deal with the case where
![]() $r\in \{t+1,t+2,\ldots ,2t+1\}$
. Let
$r\in \{t+1,t+2,\ldots ,2t+1\}$
. Let
![]() $V=\{v_{i_1},\ldots ,v_{i_x}\}$
, and let
$V=\{v_{i_1},\ldots ,v_{i_x}\}$
, and let
![]() $W_1$
be the intersection of W and V, and p the cardinality of
$W_1$
be the intersection of W and V, and p the cardinality of
![]() $W_1$
. We can assume
$W_1$
. We can assume
![]() $p\leq x-2$
, and then assume
$p\leq x-2$
, and then assume
![]() $V\backslash W_1=\{v_{j_1},\ldots ,v_{j_{x-p}}\}$
, where
$V\backslash W_1=\{v_{j_1},\ldots ,v_{j_{x-p}}\}$
, where
![]() $j_1<\cdots <j_{x-p}$
. It follows that
$j_1<\cdots <j_{x-p}$
. It follows that
![]() $W\backslash W_1$
can distinguish
$W\backslash W_1$
can distinguish
![]() $x-p-1$
pairs of vertices
$x-p-1$
pairs of vertices
![]() $(v_{j_1},v_{j_2}),\ldots ,(v_{j_{x-p-1}},v_{j_{x-p}})$
.
$(v_{j_1},v_{j_2}),\ldots ,(v_{j_{x-p-1}},v_{j_{x-p}})$
.
We remark that since
![]() $t+1\leq r\leq 2t+1$
, if a vertex w can resolve two consecutive vertices
$t+1\leq r\leq 2t+1$
, if a vertex w can resolve two consecutive vertices
![]() $v_i$
and
$v_i$
and
![]() $v_{i+1}$
, and if
$v_{i+1}$
, and if
![]() $w\neq v_i,v_{i+1}$
, then it follows from equation (1.1) that
$w\neq v_i,v_{i+1}$
, then it follows from equation (1.1) that
and
This remark shows that any vertex in
![]() $W\backslash W_1$
resolving one of the pairs of vertices
$W\backslash W_1$
resolving one of the pairs of vertices
![]() $(v_{j_1},v_{j_2}),\ldots ,(v_{j_{x-p-1}},v_{j_{x-p}})$
cannot resolve the other, implying
$(v_{j_1},v_{j_2}),\ldots ,(v_{j_{x-p-1}},v_{j_{x-p}})$
cannot resolve the other, implying
![]() $W\backslash W_1$
consists of at least
$W\backslash W_1$
consists of at least
![]() $x-p-1$
vertices, and therefore
$x-p-1$
vertices, and therefore
![]() $\sharp (W)\geq x-1$
.
$\sharp (W)\geq x-1$
.
Let us turn to the case where
![]() $r=2$
. Let
$r=2$
. Let
![]() $V^{'}=\{v_{i_1}^{'},\ldots ,v_{i_x}^{'}\}$
, and let
$V^{'}=\{v_{i_1}^{'},\ldots ,v_{i_x}^{'}\}$
, and let
![]() $W_2$
be the intersection of W and
$W_2$
be the intersection of W and
![]() $V^{'}$
. Denote by q the cardinality of
$V^{'}$
. Denote by q the cardinality of
![]() $W_2$
. We can assume that
$W_2$
. We can assume that
![]() $p+q\leq x-2$
, and then assume
$p+q\leq x-2$
, and then assume
![]() $V\backslash (W_1\cup W_2^{'})=\{v_{j_1},\ldots ,v_{j_{s}}\}$
, where
$V\backslash (W_1\cup W_2^{'})=\{v_{j_1},\ldots ,v_{j_{s}}\}$
, where
![]() $j_1<\cdots <j_{s}$
and
$j_1<\cdots <j_{s}$
and
![]() $s\geq x-p-q$
. It follows that
$s\geq x-p-q$
. It follows that
![]() $W\backslash (W_1\cup W_2)$
can distinguish
$W\backslash (W_1\cup W_2)$
can distinguish
![]() $s-1$
pairs of vertices
$s-1$
pairs of vertices
![]() $(v_{j_1},v_{j_2}),\ldots ,(v_{j_{s-1}},v_{j_{s}})$
. Similarly, any vertex in
$(v_{j_1},v_{j_2}),\ldots ,(v_{j_{s-1}},v_{j_{s}})$
. Similarly, any vertex in
![]() $W\backslash (W_1\cup W_2)$
resolving one of these pairs cannot resolve the other, implying
$W\backslash (W_1\cup W_2)$
resolving one of these pairs cannot resolve the other, implying
![]() $W\backslash (W_1\cup W_2)$
consists of at least
$W\backslash (W_1\cup W_2)$
consists of at least
![]() $s-1$
vertices, and therefore
$s-1$
vertices, and therefore
![]() $\sharp (W)\geq x-1$
.
$\sharp (W)\geq x-1$
.
The authors showed in [Reference Chau and Gosselin2] that
![]() $\dim (C_n(1,2,\ldots ,t))$
has a lower bound of
$\dim (C_n(1,2,\ldots ,t))$
has a lower bound of
![]() $t+1$
if
$t+1$
if
![]() $r\in \{2\}\cup \{t+1,t+2,\ldots ,2t\}$
. We provide an alternate proof.
$r\in \{2\}\cup \{t+1,t+2,\ldots ,2t\}$
. We provide an alternate proof.
Theorem 2.5 ([Reference Chau and Gosselin2, Theorem 2.7]) Let
![]() $n=2tk+r$
where
$n=2tk+r$
where
![]() $r\in \{2\}\cup \{t+1,t+2,\ldots ,2t\}$
. Then
$r\in \{2\}\cup \{t+1,t+2,\ldots ,2t\}$
. Then
![]() $\dim (C_n(1,2,\ldots ,t))\geq t+1$
.
$\dim (C_n(1,2,\ldots ,t))\geq t+1$
.
Proof It is sufficient to show that any resolving set W of the graph
![]() $C_n(1,2,\ldots ,t)$
has at least
$C_n(1,2,\ldots ,t)$
has at least
![]() $t+1$
vertices. Without loss of generality, we assume
$t+1$
vertices. Without loss of generality, we assume
![]() $v_0\in W$
.
$v_0\in W$
.
Let us first discuss the case where
![]() $r\in \{t+1,t+2,\ldots ,2t\}$
. Let
$r\in \{t+1,t+2,\ldots ,2t\}$
. Let
![]() $p\geq 0$
be such that
$p\geq 0$
be such that
![]() $v_{n-0},v_{n-1},\ldots ,v_{n-p}$
all belong to W while
$v_{n-0},v_{n-1},\ldots ,v_{n-p}$
all belong to W while
![]() $v_{n-p-1}\notin W$
, and let
$v_{n-p-1}\notin W$
, and let
![]() $q\geq 0$
be such that
$q\geq 0$
be such that
![]() $v_{0},v_{1},\ldots ,v_{q}$
all belong to W while
$v_{0},v_{1},\ldots ,v_{q}$
all belong to W while
![]() $v_{q+1}\notin W$
. We can assume
$v_{q+1}\notin W$
. We can assume
![]() $p+q\leq t-1$
. Set
$p+q\leq t-1$
. Set
![]() $W_1=\{v_{n-p},v_{n-p+1},\ldots ,v_{q}\}$
. Then there is a vertex
$W_1=\{v_{n-p},v_{n-p+1},\ldots ,v_{q}\}$
. Then there is a vertex
![]() $w\in W\backslash {W_1}$
that resolves
$w\in W\backslash {W_1}$
that resolves
![]() $v_{n-p-1}$
and
$v_{n-p-1}$
and
![]() $v_{q+1}$
, and therefore there exist two consecutive vertices
$v_{q+1}$
, and therefore there exist two consecutive vertices
![]() $v_i$
and
$v_i$
and
![]() $v_{i+1}$
in the
$v_{i+1}$
in the
![]() $v_{n-p-1}-v_{q+1}$
path of the outer cycle which can be resolved by w. By symmetry, assume
$v_{n-p-1}-v_{q+1}$
path of the outer cycle which can be resolved by w. By symmetry, assume
![]() $0\leq i\leq q$
. Since
$0\leq i\leq q$
. Since
![]() $r\geq t+1$
, it follows from equation (1.1) that
$r\geq t+1$
, it follows from equation (1.1) that
![]() $v_{i+1},v_{i+2},\ldots ,v_t$
have equal distance to w. Hence,
$v_{i+1},v_{i+2},\ldots ,v_t$
have equal distance to w. Hence,
![]() $W\backslash (W_1\cup \{w\})$
can distinguish
$W\backslash (W_1\cup \{w\})$
can distinguish
![]() $\{v_{q+1},\ldots ,v_{t-p}\}$
, which consists of
$\{v_{q+1},\ldots ,v_{t-p}\}$
, which consists of
![]() $t-p-q$
consecutive vertices. Applying Lemma 2.4,
$t-p-q$
consecutive vertices. Applying Lemma 2.4,
![]() $W\backslash (W_1\cup \{w\})$
has at least
$W\backslash (W_1\cup \{w\})$
has at least
![]() $t-p-q-1$
vertices, and thus W has at least
$t-p-q-1$
vertices, and thus W has at least
![]() $t+1$
vertices.
$t+1$
vertices.
The proof for the case where
![]() $r=2$
is analogous to that for the preceding case. We first note that the definitions of p and q are changed, that is, let
$r=2$
is analogous to that for the preceding case. We first note that the definitions of p and q are changed, that is, let
![]() $p\geq 0$
be such that
$p\geq 0$
be such that
![]() $v_{n-0},v_{n-1},\ldots ,v_{n-p}$
all belong to the union of W and
$v_{n-0},v_{n-1},\ldots ,v_{n-p}$
all belong to the union of W and
![]() $W^{'}$
while
$W^{'}$
while
![]() $v_{n-p-1}\notin W\cup W^{'}$
, and
$v_{n-p-1}\notin W\cup W^{'}$
, and
![]() $q\geq 0$
such that
$q\geq 0$
such that
![]() $v_{0},v_{1},\ldots ,v_{q}$
all belong to the union of W and
$v_{0},v_{1},\ldots ,v_{q}$
all belong to the union of W and
![]() $W^{'}$
while
$W^{'}$
while
![]() $v_{q+1}\notin W\cup W^{'}$
. Set
$v_{q+1}\notin W\cup W^{'}$
. Set
where
![]() $\sharp (W_2)\geq p+q+1$
. An entirely similar argument shows that there is a vertex
$\sharp (W_2)\geq p+q+1$
. An entirely similar argument shows that there is a vertex
![]() $w\in W\backslash {W_2}$
that resolves
$w\in W\backslash {W_2}$
that resolves
![]() $v_{n-p-1}$
and
$v_{n-p-1}$
and
![]() $v_{q+1}$
, and that
$v_{q+1}$
, and that
![]() $W\backslash (W_2\cup \{w\})$
has at least
$W\backslash (W_2\cup \{w\})$
has at least
![]() $t-p-q-1$
vertices, implying
$t-p-q-1$
vertices, implying
![]() $\sharp (W)\geq t+1$
.
$\sharp (W)\geq t+1$
.
In [Reference Chau and Gosselin2], the authors have shown that when
![]() $r=2t+1$
,
$r=2t+1$
,
![]() $\dim (C_n(1,2,\ldots ,t))$
has a lower bound of
$\dim (C_n(1,2,\ldots ,t))$
has a lower bound of
![]() $t+2$
. We provide an alternate proof.
$t+2$
. We provide an alternate proof.
Theorem 2.6 ([Reference Chau and Gosselin2, Theorem 2.17]) Let
![]() $n=2tk+2t+1$
. Then
$n=2tk+2t+1$
. Then
![]() $\dim (C_n(1,2,\ldots ,t))\geq t+2$
.
$\dim (C_n(1,2,\ldots ,t))\geq t+2$
.
Proof It is sufficient to show that any resolving set W for the graph
![]() $C_n(1,2,\ldots ,t)$
has at least
$C_n(1,2,\ldots ,t)$
has at least
![]() $t+2$
vertices. Without loss of generality, we assume
$t+2$
vertices. Without loss of generality, we assume
![]() $v_0\in W$
. The only vertices that can resolve
$v_0\in W$
. The only vertices that can resolve
![]() $v_{dt}$
and
$v_{dt}$
and
![]() $v_{dt+1}$
are
$v_{dt+1}$
are
By symmetry, we assume
![]() $v_{n-pt}\in W$
, where
$v_{n-pt}\in W$
, where
![]() $p\in \{1,2,\ldots ,d\}$
. We shall consider two cases.
$p\in \{1,2,\ldots ,d\}$
. We shall consider two cases.
Case 1 (
![]() $p\leq k$
): The only vertices that can resolve
$p\leq k$
): The only vertices that can resolve
![]() $v_{dt+1}$
and
$v_{dt+1}$
and
![]() $v_{dt+2}$
are
$v_{dt+2}$
are
If
![]() $v_{qt+1}\in W$
for some
$v_{qt+1}\in W$
for some
![]() $q\in \{1,\ldots ,d\}$
, one can easily verify that
$q\in \{1,\ldots ,d\}$
, one can easily verify that
![]() $\{v_0,v_{qt+1},v_{n-pt}\}$
cannot distinguish any pair of vertices in
$\{v_0,v_{qt+1},v_{n-pt}\}$
cannot distinguish any pair of vertices in
![]() $\{v_1,v_2,\ldots ,v_t\}$
. It follows from Lemma 2.4 that
$\{v_1,v_2,\ldots ,v_t\}$
. It follows from Lemma 2.4 that
![]() $W\backslash \{v_0,v_{qt+1},v_{n-pt}\}$
has at least
$W\backslash \{v_0,v_{qt+1},v_{n-pt}\}$
has at least
![]() $t-1$
vertices, which confirms the assertion. If
$t-1$
vertices, which confirms the assertion. If
![]() $v_{n+1-qt}\in W$
for some
$v_{n+1-qt}\in W$
for some
![]() $q\in \{1,\ldots ,d\}$
, it is easy to see that
$q\in \{1,\ldots ,d\}$
, it is easy to see that
![]() $\{v_0,v_{n+1-qt},v_{n-pt}\}$
cannot distinguish any pair of vertices in
$\{v_0,v_{n+1-qt},v_{n-pt}\}$
cannot distinguish any pair of vertices in
![]() $\{v_{(d-q)t+1},v_{(d-q)t+2},\ldots ,v_{(d-q+1)t}\}$
, and according to Lemma 2.4,
$\{v_{(d-q)t+1},v_{(d-q)t+2},\ldots ,v_{(d-q+1)t}\}$
, and according to Lemma 2.4,
![]() $W\backslash \{v_0,v_{n+1-qt},v_{n-pt}\}$
has at least
$W\backslash \{v_0,v_{n+1-qt},v_{n-pt}\}$
has at least
![]() $t-1$
vertices, and therefore W has at least
$t-1$
vertices, and therefore W has at least
![]() $t+2$
vertices.
$t+2$
vertices.
Case 2 (
![]() $p=d$
): The only vertices that can resolve
$p=d$
): The only vertices that can resolve
![]() $v_{kt+1}$
and
$v_{kt+1}$
and
![]() $v_{kt+2}$
are
$v_{kt+2}$
are
If
![]() $v_{qt+1}\in W$
for some
$v_{qt+1}\in W$
for some
![]() $q\in \{1,2,\ldots ,k\}$
, one can verify that
$q\in \{1,2,\ldots ,k\}$
, one can verify that
![]() $\{v_0,v_{qt+1},v_{n-dt}\}$
cannot distinguish any pair of vertices in
$\{v_0,v_{qt+1},v_{n-dt}\}$
cannot distinguish any pair of vertices in
![]() $\{v_1,v_2,\ldots ,v_t\}$
. If
$\{v_1,v_2,\ldots ,v_t\}$
. If
![]() $v_{n+1-qt}\in W$
for some
$v_{n+1-qt}\in W$
for some
![]() $q\in \{2,3,\ldots ,d\}$
, one can verify that
$q\in \{2,3,\ldots ,d\}$
, one can verify that
![]() $\{v_0,v_{n+1-qt},v_{n-dt}\}$
cannot distinguish any pair of vertices in
$\{v_0,v_{n+1-qt},v_{n-dt}\}$
cannot distinguish any pair of vertices in
![]() $\{v_{(d-q)t+1},v_{(d-q)t+2},\ldots ,v_{(d-q+1)t}\}$
. If
$\{v_{(d-q)t+1},v_{(d-q)t+2},\ldots ,v_{(d-q+1)t}\}$
. If
![]() $v_{kt+2}\in W$
, then it is easy to see that
$v_{kt+2}\in W$
, then it is easy to see that
![]() $\{v_0,v_{kt+2},v_{n-dt}\}$
cannot distinguish any pair of vertices in
$\{v_0,v_{kt+2},v_{n-dt}\}$
cannot distinguish any pair of vertices in
![]() $\{v_{n-(t-1)},\ldots ,v_{n-2},v_{n-1},v_1\}$
, which consists of t vertices coming from a clique of
$\{v_{n-(t-1)},\ldots ,v_{n-2},v_{n-1},v_1\}$
, which consists of t vertices coming from a clique of
![]() $t+1$
consecutive vertices. If
$t+1$
consecutive vertices. If
![]() $v_{1}\in W$
, then
$v_{1}\in W$
, then
![]() $\{v_0,v_{1},v_{n-dt}\}$
cannot distinguish any pair of vertices in
$\{v_0,v_{1},v_{n-dt}\}$
cannot distinguish any pair of vertices in
![]() $\{v_{dt},v_{dt+2},v_{dt+3},\ldots ,v_{dt+t}\}$
. In both cases, it follows quickly from Lemma 2.4 that W has at least
$\{v_{dt},v_{dt+2},v_{dt+3},\ldots ,v_{dt+t}\}$
. In both cases, it follows quickly from Lemma 2.4 that W has at least
![]() $(t-1)+3=t+2$
vertices. The proof is complete.
$(t-1)+3=t+2$
vertices. The proof is complete.
3 Upper bounds
This section is devoted to the study of upper bounds for
![]() $\dim (C_n(1,2,\ldots ,t))$
. The following three theorems provide a great deal of useful information about this topic.
$\dim (C_n(1,2,\ldots ,t))$
. The following three theorems provide a great deal of useful information about this topic.
Theorem 3.1 ([Reference Grigorious, Manuel, Miller, Rajan and Stephen4, Theorem 2.9]) Let
![]() $n=2tk+r$
where
$n=2tk+r$
where
![]() $2\leq r\leq t+1$
. Then
$2\leq r\leq t+1$
. Then
Theorem 3.2 ([Reference Vetrík10, Theorem 2.1 and Theorem 2.2]) Let
![]() $n=2tk+t+p$
where t and p are both even, and
$n=2tk+t+p$
where t and p are both even, and
![]() $0\leq p\leq t$
. Then
$0\leq p\leq t$
. Then
Theorem 3.3 ([Reference Vetrík12, Theorem 5]) Let
![]() $n=2tk+t+p$
where t is even, p is odd, and
$n=2tk+t+p$
where t is even, p is odd, and
![]() $1\leq p\leq t+1$
. Then
$1\leq p\leq t+1$
. Then
Motivated by the work of Vetrík, we provide an upper bound on the metric dimension of
![]() $C_n(1,2,\ldots ,t)$
, where t is odd and
$C_n(1,2,\ldots ,t)$
, where t is odd and
![]() $r\geq t+2$
.
$r\geq t+2$
.
Theorem 3.4 Let
![]() $n=2tk+t+p$
where t is odd, p is even, and
$n=2tk+t+p$
where t is odd, p is even, and
![]() $2\leq p\leq t+1$
. Then
$2\leq p\leq t+1$
. Then
Proof Let
where
![]() $\sharp (W_1)=\frac {t+1}{2}$
and
$\sharp (W_1)=\frac {t+1}{2}$
and
![]() $\sharp (W_2)=\frac {t+p-1}{2}$
. Let us show that
$\sharp (W_2)=\frac {t+p-1}{2}$
. Let us show that
![]() $W=W_1\cup W_2$
is a resolving set of the graph
$W=W_1\cup W_2$
is a resolving set of the graph
![]() $C_n(1,2,\ldots ,t)$
. Divide the vertex set of
$C_n(1,2,\ldots ,t)$
. Divide the vertex set of
![]() $C_n(1,2,\ldots ,t)$
into four disjoint sets:
$C_n(1,2,\ldots ,t)$
into four disjoint sets:
 $$ \begin{align*} &V_1=\{v_0,v_1,\ldots,v_t\}, V_2=\{v_{t+1},v_{t+2},\ldots,v_{kt-1},v_{kt}\},\\ &V_3=\{v_{kt+1},v_{kt+2},\ldots,v_{kt+t+p-2},v_{kt+t+p-1}\},V_4=\{v_{kt+t+p},v_{kt+t+p+1},\ldots,v_{n-2},v_{n-1}\}. \end{align*} $$
$$ \begin{align*} &V_1=\{v_0,v_1,\ldots,v_t\}, V_2=\{v_{t+1},v_{t+2},\ldots,v_{kt-1},v_{kt}\},\\ &V_3=\{v_{kt+1},v_{kt+2},\ldots,v_{kt+t+p-2},v_{kt+t+p-1}\},V_4=\{v_{kt+t+p},v_{kt+t+p+1},\ldots,v_{n-2},v_{n-1}\}. \end{align*} $$
We claim that any pair of distinct vertices
![]() $u\in V_{r_1}$
and
$u\in V_{r_1}$
and
![]() $v\in V_{r_2}$
have different metric representations with respect to W. We need only consider the following six cases, since in other cases, it is easy to check that
$v\in V_{r_2}$
have different metric representations with respect to W. We need only consider the following six cases, since in other cases, it is easy to check that
![]() $v_0$
can resolve u and v.
$v_0$
can resolve u and v.
Case 1 (
![]() $r_1=r_2=1$
): It suffices to prove that no two vertices in
$r_1=r_2=1$
): It suffices to prove that no two vertices in
![]() $V_1\backslash W_1=\{v_j:j=1,3,\ldots ,t\}$
have the same metric representation with respect to
$V_1\backslash W_1=\{v_j:j=1,3,\ldots ,t\}$
have the same metric representation with respect to
![]() $W_{21}:=\{v_{kt+2},v_{kt+4},\ldots ,v_{kt+t-1}\}$
;
$W_{21}:=\{v_{kt+2},v_{kt+4},\ldots ,v_{kt+t-1}\}$
;
![]() $W_{21}$
is obviously a subset of
$W_{21}$
is obviously a subset of
![]() $W_2$
. We observe that for
$W_2$
. We observe that for
![]() $j=1,3,\ldots ,t$
,
$j=1,3,\ldots ,t$
,
![]() $r(v_j|W_{21})=(k,\ldots ,k,k+1,\ldots ,k+1)$
, of which the first
$r(v_j|W_{21})=(k,\ldots ,k,k+1,\ldots ,k+1)$
, of which the first
![]() $\frac {j-1}{2}$
entries are equal to k, and the other
$\frac {j-1}{2}$
entries are equal to k, and the other
![]() $\frac {t-j}{2}$
entries are equal to
$\frac {t-j}{2}$
entries are equal to
![]() $k+1$
, the desired result follows.
$k+1$
, the desired result follows.
Case 2 (
![]() $r_1=r_2=2$
): For
$r_1=r_2=2$
): For
![]() $x=1,\ldots ,k-1$
and
$x=1,\ldots ,k-1$
and
![]() $j=1,2,\ldots ,t$
, the metric representation of
$j=1,2,\ldots ,t$
, the metric representation of
![]() $v_{tx+j}\in V_2$
with respect to
$v_{tx+j}\in V_2$
with respect to
![]() $W_1$
is
$W_1$
is
 $$ \begin{align*}r(v_{tx+j}|W_1)=(\underbrace{x+1,\ldots,x+1}_{\left\lceil\frac{j}{2}\right\rceil},\underbrace{x,\ldots,x}_{\frac{t+1}{2}-\left\lceil\frac{j}{2}\right\rceil}). \end{align*} $$
$$ \begin{align*}r(v_{tx+j}|W_1)=(\underbrace{x+1,\ldots,x+1}_{\left\lceil\frac{j}{2}\right\rceil},\underbrace{x,\ldots,x}_{\frac{t+1}{2}-\left\lceil\frac{j}{2}\right\rceil}). \end{align*} $$
Hence, the only vertices in
![]() $V_2$
with the same metric representations with respect to
$V_2$
with the same metric representations with respect to
![]() $W_1$
are the pairs
$W_1$
are the pairs
![]() $(v_{tx+j-1},v_{tx+j})$
, where
$(v_{tx+j-1},v_{tx+j})$
, where
![]() $j=2,4,\ldots ,t-1$
and
$j=2,4,\ldots ,t-1$
and
![]() $x=1,2,\ldots ,k-1$
. Since
$x=1,2,\ldots ,k-1$
. Since
![]() $v_{kt+j}$
belongs to
$v_{kt+j}$
belongs to
![]() $W_2$
for each
$W_2$
for each
![]() $j\in \{2,4,\ldots ,t-1\}$
, and since
$j\in \{2,4,\ldots ,t-1\}$
, and since
it follows that
![]() $W_2$
can distinguish all these pairs.
$W_2$
can distinguish all these pairs.
Case 3 (
![]() $r_1=r_2=3$
): Note that
$r_1=r_2=3$
): Note that
 $$ \begin{align*} &r(v_{kt+j}|W_1)=(\overbrace{k+1,\ldots,k+1}^{\left\lceil\frac{j}{2}\right\rceil},\overbrace{k,\ldots,k}^{\frac{t+1}{2}-\left\lceil\frac{j}{2}\right\rceil})\quad\text{for}\,\, j=1,2,\ldots,t-1, \\ &r(v_{kt+j}|W_1)=(k+1,\ldots,k+1)\quad\text{for}\,\,j=t,t+1,\ldots,t+p-1. \end{align*} $$
$$ \begin{align*} &r(v_{kt+j}|W_1)=(\overbrace{k+1,\ldots,k+1}^{\left\lceil\frac{j}{2}\right\rceil},\overbrace{k,\ldots,k}^{\frac{t+1}{2}-\left\lceil\frac{j}{2}\right\rceil})\quad\text{for}\,\, j=1,2,\ldots,t-1, \\ &r(v_{kt+j}|W_1)=(k+1,\ldots,k+1)\quad\text{for}\,\,j=t,t+1,\ldots,t+p-1. \end{align*} $$
Write
![]() $u=v_{kt+j_1}$
and
$u=v_{kt+j_1}$
and
![]() $v=v_{kt+j_2}$
. We need only consider the following two subcases, since in other cases,
$v=v_{kt+j_2}$
. We need only consider the following two subcases, since in other cases,
![]() $v_{t-1}\in W_1$
can already resolve u and v.
$v_{t-1}\in W_1$
can already resolve u and v.
Case 3.1 (
![]() $j_1<t$
,
$j_1<t$
,
![]() $j_2<t$
): In this case, the only vertices with the same metric representations with respect to
$j_2<t$
): In this case, the only vertices with the same metric representations with respect to
![]() $W_1$
are the pairs
$W_1$
are the pairs
![]() $(v_{kt+j-1},v_{kt+j})$
, where
$(v_{kt+j-1},v_{kt+j})$
, where
![]() $j=2,4,\ldots ,t-1$
. Since
$j=2,4,\ldots ,t-1$
. Since
![]() $W_2$
contains
$W_2$
contains
![]() $v_{kt+j}$
for each
$v_{kt+j}$
for each
![]() $j\in \{2,4,\ldots ,t-1\}$
, it follows that
$j\in \{2,4,\ldots ,t-1\}$
, it follows that
![]() $W_2$
can distinguish these pairs.
$W_2$
can distinguish these pairs.
Case 3.2 (
![]() $j_1\geq t$
,
$j_1\geq t$
,
![]() $j_2\geq t$
): Recalling the construction of
$j_2\geq t$
): Recalling the construction of
![]() $W_2$
, we need only show that no two vertices in
$W_2$
, we need only show that no two vertices in
![]() $\{v_{kt+t+j}:j=0,2,\ldots ,p-2\}\cup \{v_{kt+t+p-1}\}$
have the same metric representation with respect to
$\{v_{kt+t+j}:j=0,2,\ldots ,p-2\}\cup \{v_{kt+t+p-1}\}$
have the same metric representation with respect to
![]() $W_{22}:=\{v_{kt},v_{kt+2},\ldots ,v_{kt+p-2}\}$
;
$W_{22}:=\{v_{kt},v_{kt+2},\ldots ,v_{kt+p-2}\}$
;
![]() $W_{22}$
is obviously a subset of
$W_{22}$
is obviously a subset of
![]() $W_2$
. We observe that
$W_2$
. We observe that
![]() $r(v_{kt+t+j}|W_{22})=(2,\ldots ,2,1,\ldots ,1)$
,
$r(v_{kt+t+j}|W_{22})=(2,\ldots ,2,1,\ldots ,1)$
,
![]() $j=0,2,\ldots ,p-2$
, of which the first
$j=0,2,\ldots ,p-2$
, of which the first
![]() $\frac {j}{2}$
entries are equal to
$\frac {j}{2}$
entries are equal to
![]() $2$
and the other
$2$
and the other
![]() $\frac {p-j}{2}$
entries are equal to
$\frac {p-j}{2}$
entries are equal to
![]() $1$
, and that all the distances from
$1$
, and that all the distances from
![]() $v_{kt+t+p-1}$
to the vertices in
$v_{kt+t+p-1}$
to the vertices in
![]() $W_{22}$
are
$W_{22}$
are
![]() $2$
; the desired result follows.
$2$
; the desired result follows.
Case 4 (
![]() $r_1=r_2=4$
): It is not difficult to see that for
$r_1=r_2=4$
): It is not difficult to see that for
![]() $x=1,2,\ldots ,k$
and
$x=1,2,\ldots ,k$
and
![]() $j=0,1,\ldots ,t-1$
, the metric representation of
$j=0,1,\ldots ,t-1$
, the metric representation of
![]() $v_{n-tx+j}\in V_4$
with respect to
$v_{n-tx+j}\in V_4$
with respect to
![]() $W_1$
is
$W_1$
is
 $$ \begin{align*}r(v_{n-tx+j}|W_1)=(\underbrace{x,\ldots,x}_{\left\lfloor\frac{j}{2}\right\rfloor+1},\underbrace{x+1,\ldots,x+1}_{\frac{t-1}{2}-\left\lfloor\frac{j}{2}\right\rfloor}). \end{align*} $$
$$ \begin{align*}r(v_{n-tx+j}|W_1)=(\underbrace{x,\ldots,x}_{\left\lfloor\frac{j}{2}\right\rfloor+1},\underbrace{x+1,\ldots,x+1}_{\frac{t-1}{2}-\left\lfloor\frac{j}{2}\right\rfloor}). \end{align*} $$
Thus, the only vertices in
![]() $V_4$
with the same metric representations with respect to
$V_4$
with the same metric representations with respect to
![]() $W_1$
are the pairs
$W_1$
are the pairs
![]() $(v_{n-tx+j},v_{n-tx+j+1})$
, where
$(v_{n-tx+j},v_{n-tx+j+1})$
, where
![]() $j=0,2,\ldots ,t-3$
and
$j=0,2,\ldots ,t-3$
and
![]() $x=1,2,\ldots ,k$
. Since
$x=1,2,\ldots ,k$
. Since
![]() $v_{n-kt-t+j}$
belongs to
$v_{n-kt-t+j}$
belongs to
![]() $W_2$
for each
$W_2$
for each
![]() $j\in \{0,2,\ldots ,t-3\}$
, and since
$j\in \{0,2,\ldots ,t-3\}$
, and since
it follows that
![]() $W_2$
can distinguish these pairs.
$W_2$
can distinguish these pairs.
Case 5 (
![]() $r_1=1$
,
$r_1=1$
,
![]() $r_2=4$
): The distances from the vertices in
$r_2=4$
): The distances from the vertices in
![]() $V_1$
to
$V_1$
to
![]() $v_{kt}$
are at most k, and the distances from the vertices in
$v_{kt}$
are at most k, and the distances from the vertices in
![]() $V_4$
to
$V_4$
to
![]() $v_{kt}$
are
$v_{kt}$
are
![]() $k+1$
, and therefore
$k+1$
, and therefore
![]() $v_{kt}$
can resolve u and v.
$v_{kt}$
can resolve u and v.
Case 6 (
![]() $r_1=2$
,
$r_1=2$
,
![]() $r_2=4$
): In this case, it is clear that the only vertices with the same metric representations with respect to
$r_2=4$
): In this case, it is clear that the only vertices with the same metric representations with respect to
![]() $W_1$
are the pairs
$W_1$
are the pairs
![]() $(v_{tx+t},v_{n-tx-1})$
, where
$(v_{tx+t},v_{n-tx-1})$
, where
![]() $x=1,2,\ldots ,k-1$
. Since
$x=1,2,\ldots ,k-1$
. Since
it follows that
![]() $v_{kt}\in W_2$
can resolve all these pairs.
$v_{kt}\in W_2$
can resolve all these pairs.
Theorem 3.5 Let
![]() $n=2tk+t+p$
where t and p are both odd, and
$n=2tk+t+p$
where t and p are both odd, and
![]() $3\leq p\leq t$
. Then
$3\leq p\leq t$
. Then
Proof Let
 $$ \begin{align*} &W_1=\{v_0,v_2,\ldots,v_{t-1}\}, W_2=\{v_{n-(t-1)},v_{n-(t-3)},\ldots,v_{n-2}\},\\ &W_3=\{v_{kt+1},v_{kt+3},\ldots,v_{kt+p-2}\}, \end{align*} $$
$$ \begin{align*} &W_1=\{v_0,v_2,\ldots,v_{t-1}\}, W_2=\{v_{n-(t-1)},v_{n-(t-3)},\ldots,v_{n-2}\},\\ &W_3=\{v_{kt+1},v_{kt+3},\ldots,v_{kt+p-2}\}, \end{align*} $$
where
![]() $\sharp (W_1)=\frac {t+1}{2}$
,
$\sharp (W_1)=\frac {t+1}{2}$
,
![]() $\sharp (W_2)=\frac {t-1}{2}$
, and
$\sharp (W_2)=\frac {t-1}{2}$
, and
![]() $\sharp (W_3)=\frac {p-1}{2}$
. Let us show that
$\sharp (W_3)=\frac {p-1}{2}$
. Let us show that
![]() $W=W_1\cup W_2\cup W_3$
is a resolving set of the graph
$W=W_1\cup W_2\cup W_3$
is a resolving set of the graph
![]() $C_n(1,2,\ldots ,t)$
. As before, divide the vertex set of
$C_n(1,2,\ldots ,t)$
. As before, divide the vertex set of
![]() $C_n(1,2,\ldots ,t)$
into four disjoint sets:
$C_n(1,2,\ldots ,t)$
into four disjoint sets:
 $$ \begin{align*} &V_1=\{v_0,v_1,\ldots,v_t\}, V_2=\{v_{t+1},v_{t+2},\ldots,v_{kt-1},v_{kt}\},\\ &V_3=\{v_{kt+1},v_{kt+2},\ldots,v_{kt+t+p-2},v_{kt+t+p-1}\},V_4=\{v_{kt+t+p},v_{kt+t+p+1},\ldots,v_{n-2},v_{n-1}\}. \end{align*} $$
$$ \begin{align*} &V_1=\{v_0,v_1,\ldots,v_t\}, V_2=\{v_{t+1},v_{t+2},\ldots,v_{kt-1},v_{kt}\},\\ &V_3=\{v_{kt+1},v_{kt+2},\ldots,v_{kt+t+p-2},v_{kt+t+p-1}\},V_4=\{v_{kt+t+p},v_{kt+t+p+1},\ldots,v_{n-2},v_{n-1}\}. \end{align*} $$
We claim that any pair of distinct vertices
![]() $u\in V_{r_1}$
and
$u\in V_{r_1}$
and
![]() $v\in V_{r_2}$
have different metric representations with respect to W, and only consider six cases.
$v\in V_{r_2}$
have different metric representations with respect to W, and only consider six cases.
Case 1 (
![]() $r_1=r_2=1$
): We need only show that no two vertices in
$r_1=r_2=1$
): We need only show that no two vertices in
![]() $V_1\backslash W_1=\{v_j:j=1,3,\ldots ,t\}$
have the same metric representation with respect to
$V_1\backslash W_1=\{v_j:j=1,3,\ldots ,t\}$
have the same metric representation with respect to
![]() $W_2$
. Observe that for
$W_2$
. Observe that for
![]() $j=1,3,\ldots ,t$
,
$j=1,3,\ldots ,t$
,
![]() $r(v_j|W_2)=(2,\ldots ,2,1,\ldots ,1)$
, of which the first
$r(v_j|W_2)=(2,\ldots ,2,1,\ldots ,1)$
, of which the first
![]() $\frac {j-1}{2}$
entries are equal to
$\frac {j-1}{2}$
entries are equal to
![]() $2$
, and the other
$2$
, and the other
![]() $\frac {t-j}{2}$
entries are equal to
$\frac {t-j}{2}$
entries are equal to
![]() $1$
, the desired result follows.
$1$
, the desired result follows.
Case 2 (
![]() $r_1=r_2=2$
): It is easy to verify that, for
$r_1=r_2=2$
): It is easy to verify that, for
![]() $x=1,\ldots ,k-1$
and
$x=1,\ldots ,k-1$
and
![]() $j=1,2,\ldots ,t$
, the metric representation of
$j=1,2,\ldots ,t$
, the metric representation of
![]() $v_{tx+j}\in V_2$
with respect to
$v_{tx+j}\in V_2$
with respect to
![]() $W_1$
is
$W_1$
is
 $$ \begin{align*}r(v_{tx+j}|W_1)=(\underbrace{x+1,\ldots,x+1}_{\left\lceil\frac{j}{2}\right\rceil},\underbrace{x,\ldots,x}_{\frac{t+1}{2}-\left\lceil\frac{j}{2}\right\rceil}). \end{align*} $$
$$ \begin{align*}r(v_{tx+j}|W_1)=(\underbrace{x+1,\ldots,x+1}_{\left\lceil\frac{j}{2}\right\rceil},\underbrace{x,\ldots,x}_{\frac{t+1}{2}-\left\lceil\frac{j}{2}\right\rceil}). \end{align*} $$
Hence, the only vertices in
![]() $V_2$
with the same metric representations with respect to
$V_2$
with the same metric representations with respect to
![]() $W_1$
are the pairs
$W_1$
are the pairs
![]() $(v_{tx+j},v_{tx+j+1})$
, where
$(v_{tx+j},v_{tx+j+1})$
, where
![]() $j=1,3,\ldots ,t-2$
and
$j=1,3,\ldots ,t-2$
and
![]() $x=1,2,\ldots ,k-1$
. Since
$x=1,2,\ldots ,k-1$
. Since
![]() $v_{n-t+j}$
belongs to
$v_{n-t+j}$
belongs to
![]() $W_2$
for each
$W_2$
for each
![]() $j\in \{1,3,\ldots ,t-2\}$
, and since
$j\in \{1,3,\ldots ,t-2\}$
, and since
it follows that
![]() $W_2$
can distinguish these pairs.
$W_2$
can distinguish these pairs.
Case 3 (
![]() $r_1=r_2=3$
): The metric representations of the vertices in
$r_1=r_2=3$
): The metric representations of the vertices in
![]() $V_3$
with respect to
$V_3$
with respect to
![]() $W_1$
and
$W_1$
and
![]() $W_2$
are the following:
$W_2$
are the following:
 $$ \begin{align*} &r(v_{kt+j}|W_1)=(\overbrace{k+1,\ldots,k+1}^{\left\lceil\frac{j}{2}\right\rceil},\overbrace{k,\ldots,k}^{\frac{t+1}{2}-\left\lceil\frac{j}{2}\right\rceil}) \quad\text{for}\,\, j=1,2,\ldots,t-1, \\ &r(v_{kt+j}|W_1)=(k+1,\ldots,k+1)\quad\text{for}\,\, j=t,t+1,\ldots,t+p-1,\\ &r(v_{kt+j}|W_2)=(k+1,\ldots,k+1)\quad\text{for}\,\, j=1,2,\ldots,p-1,\\ &r(v_{kt+j}|W_2)=(\underbrace{k,\ldots,k}_{\left\lceil\frac{j-p}{2}\right\rceil},\underbrace{k+1,\ldots,k+1}_{\frac{t-1}{2}-\left\lceil\frac{j-p}{2}\right\rceil})\quad\text{for}\,\, j=p,p+1,\ldots,t+p-1. \end{align*} $$
$$ \begin{align*} &r(v_{kt+j}|W_1)=(\overbrace{k+1,\ldots,k+1}^{\left\lceil\frac{j}{2}\right\rceil},\overbrace{k,\ldots,k}^{\frac{t+1}{2}-\left\lceil\frac{j}{2}\right\rceil}) \quad\text{for}\,\, j=1,2,\ldots,t-1, \\ &r(v_{kt+j}|W_1)=(k+1,\ldots,k+1)\quad\text{for}\,\, j=t,t+1,\ldots,t+p-1,\\ &r(v_{kt+j}|W_2)=(k+1,\ldots,k+1)\quad\text{for}\,\, j=1,2,\ldots,p-1,\\ &r(v_{kt+j}|W_2)=(\underbrace{k,\ldots,k}_{\left\lceil\frac{j-p}{2}\right\rceil},\underbrace{k+1,\ldots,k+1}_{\frac{t-1}{2}-\left\lceil\frac{j-p}{2}\right\rceil})\quad\text{for}\,\, j=p,p+1,\ldots,t+p-1. \end{align*} $$
Write
![]() $u=v_{kt+j_1}$
and
$u=v_{kt+j_1}$
and
![]() $v=v_{kt+j_2}$
. There are two subcases to consider.
$v=v_{kt+j_2}$
. There are two subcases to consider.
Case 3.1 (
![]() $j_1<t$
,
$j_1<t$
,
![]() $j_2<t$
): In this case, the only vertices with the same metric representations with respect to
$j_2<t$
): In this case, the only vertices with the same metric representations with respect to
![]() $W_1$
are the pairs
$W_1$
are the pairs
![]() $(v_{kt+j},v_{kt+j+1})$
, where
$(v_{kt+j},v_{kt+j+1})$
, where
![]() $j=1,3,\ldots ,t-2$
. If
$j=1,3,\ldots ,t-2$
. If
![]() $p=t$
, then
$p=t$
, then
![]() $W_3$
can already distinguish all the pairs. Suppose now that
$W_3$
can already distinguish all the pairs. Suppose now that
![]() $p\leq t-2$
. In view of the definition of
$p\leq t-2$
. In view of the definition of
![]() $W_3$
, it is sufficient to show that
$W_3$
, it is sufficient to show that
![]() $(v_{kt+j},v_{kt+j+1})$
can be distinguished by
$(v_{kt+j},v_{kt+j+1})$
can be distinguished by
![]() $W_2$
for
$W_2$
for
![]() $j=p,p+2,\ldots ,t-2$
. Noticing that
$j=p,p+2,\ldots ,t-2$
. Noticing that
![]() $v_{2kt+j+1}$
belongs to
$v_{2kt+j+1}$
belongs to
![]() $W_2$
for each
$W_2$
for each
![]() $j\in \{p,p+2,\ldots ,t-2\}$
, and that
$j\in \{p,p+2,\ldots ,t-2\}$
, and that
the desired result follows.
Case 3.2 (
![]() $j_1\geq t$
,
$j_1\geq t$
,
![]() $j_2\geq t$
): In this case, the only vertices with the same metric representations with respect to
$j_2\geq t$
): In this case, the only vertices with the same metric representations with respect to
![]() $W_2$
are the pairs
$W_2$
are the pairs
![]() $(v_{kt+t+j},v_{kt+t+j+1})$
, where
$(v_{kt+t+j},v_{kt+t+j+1})$
, where
![]() $j=1,3,\ldots , p-2$
. Since
$j=1,3,\ldots , p-2$
. Since
![]() $v_{kt+j}$
belongs to
$v_{kt+j}$
belongs to
![]() $W_3$
for each
$W_3$
for each
![]() $j\in \{1,3,\ldots ,p-2\}$
, and since
$j\in \{1,3,\ldots ,p-2\}$
, and since
it follows that
![]() $W_3$
can distinguish these pairs.
$W_3$
can distinguish these pairs.
Case 4 (
![]() $r_1=r_2=4$
): For
$r_1=r_2=4$
): For
![]() $x=1,2,\ldots ,k$
and
$x=1,2,\ldots ,k$
and
![]() $j=0,1,\ldots ,t-1$
, the metric representation of
$j=0,1,\ldots ,t-1$
, the metric representation of
![]() $v_{n-tx+j}\in V_4$
with respect to
$v_{n-tx+j}\in V_4$
with respect to
![]() $W_1$
is
$W_1$
is
 $$ \begin{align*}r(v_{n-tx+j}|W_1)=(\underbrace{x,\ldots,x}_{\left\lfloor\frac{j}{2}\right\rfloor+1},\underbrace{x+1,\ldots,x+1}_{\frac{t-1}{2}-\left\lfloor\frac{j}{2}\right\rfloor}). \end{align*} $$
$$ \begin{align*}r(v_{n-tx+j}|W_1)=(\underbrace{x,\ldots,x}_{\left\lfloor\frac{j}{2}\right\rfloor+1},\underbrace{x+1,\ldots,x+1}_{\frac{t-1}{2}-\left\lfloor\frac{j}{2}\right\rfloor}). \end{align*} $$
Hence, the only vertices in
![]() $V_4$
with the same metric representations with respect to
$V_4$
with the same metric representations with respect to
![]() $W_1$
are the pairs
$W_1$
are the pairs
![]() $(v_{n-tx+j-1},v_{n-tx+j})$
, where
$(v_{n-tx+j-1},v_{n-tx+j})$
, where
![]() $j=1,3,\ldots ,t-2$
and
$j=1,3,\ldots ,t-2$
and
![]() $x=1,2,\ldots ,k$
. Since
$x=1,2,\ldots ,k$
. Since
![]() $v_{n-t+j}$
belongs to
$v_{n-t+j}$
belongs to
![]() $W_2$
for each
$W_2$
for each
![]() $j\in \{1,3,\ldots ,t-2\}$
, and since
$j\in \{1,3,\ldots ,t-2\}$
, and since
it follows that
![]() $W_2$
can distinguish all these pairs.
$W_2$
can distinguish all these pairs.
Case 5 (
![]() $r_1=1$
,
$r_1=1$
,
![]() $r_2=4$
): In this case, the only vertices with the same metric representations with respect to
$r_2=4$
): In this case, the only vertices with the same metric representations with respect to
![]() $W_1$
are the pairs
$W_1$
are the pairs
![]() $(v_{n-1},v_{j})$
, where
$(v_{n-1},v_{j})$
, where
![]() $j=1,3,\ldots ,t$
, which can be resolved by
$j=1,3,\ldots ,t$
, which can be resolved by
![]() $v_{kt+1}\in W_3$
.
$v_{kt+1}\in W_3$
.
Case 6 (
![]() $r_1=2$
,
$r_1=2$
,
![]() $r_2=4$
): In this case, the only vertices with the same metric representations with respect to
$r_2=4$
): In this case, the only vertices with the same metric representations with respect to
![]() $W_1$
are the pairs
$W_1$
are the pairs
![]() $(v_{tx+t},v_{n-tx-1})$
, where
$(v_{tx+t},v_{n-tx-1})$
, where
![]() $x=1,2,\ldots ,k-1$
. Note that
$x=1,2,\ldots ,k-1$
. Note that
![]() $v_{n-2}$
belongs to
$v_{n-2}$
belongs to
![]() $W_2$
, and that
$W_2$
, and that
Therefore,
![]() $W_2$
can distinguish these pairs. This completes our proof.
$W_2$
can distinguish these pairs. This completes our proof.