Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T21:43:46.192Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Maximal Operator Ideal Associated with a Tensor Norm Defined by Interpolation Spaces

Published online by Cambridge University Press:  20 November 2018

M. E. Puerta  and
G. Loaiza
M. E. Puerta
Affiliation:
Universidad EAFIT, Departamento de Ciencias Bsicas, Medelln, Colombia e-mail: [email protected]@eafit.edu.co
G. Loaiza
Affiliation:
Universidad EAFIT, Departamento de Ciencias Bsicas, Medelln, Colombia e-mail: [email protected]@eafit.edu.co
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The classical approach to studying operator ideals using tensor norms mainly focuses on those tensor norms and operator ideals defined by means of 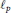${{l}_{p}}$ spaces. In a previous paper, an interpolation space, defined via the real method and using 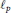${{l}_{p}}$ spaces, was used to define a tensor norm, and the associated minimal operator ideals were characterized. In this paper, the next natural step is taken, that is, the corresponding maximal operator ideals are characterized. As an application, necessary and sufficient conditions for the coincidence of the maximal and minimal ideals are given. Finally, the previous results are used in order to find some new metric properties of the mentioned tensor norm.

Keywords

46M0546M3546A32maximal operator idealsultraproducts of spacesinterpolation spaces
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 53 , Issue 4 , 01 December 2010 , pp. 690 - 705
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Aliprantis, C. D. and Burkinshaw, O., Positive operators. Pure and Applied Mathematics, 119, Academic Press, Inc., Orlando, FL, 1985.Google Scholar
[2] Arango, G., Molina, J. A. López, and Rivera, M. J., Characterization of g∞, p -integral operators. Math. Nachr. 278(2005), no. 9, 995–1014. doi:10.1002/mana.200310286Google Scholar
[3] Beauzamy, B., Espaces d’interpolation reéls: topologie et géométrie. Lecture Notes in Mathematics, 666, Springer, Berlin, 1978.Google Scholar
[4] Bergh, J. and Lofstrom, J., Interpolation spaces. An introduction. Grundlehren der Mathematischen Wissenschaften, 223, Springer-Verlag, Berlin-New York, 1976.Google Scholar
[5] Creekmore, J., Type and cotype in Lorentz Lpq spaces. Nederl. Akad.Wetensch. Indag. Math. 43(1981), no. 2, 145–152.Google Scholar
[6] De Grande-De Kimpe, N., Λ-mappings between locally convex spaces. Indag. Math. 33(1971), 261–274.Google Scholar
[7] Defant, A. and Floret, K., Tensor norms and operator ideals. North-Holland Mathematics Studies, 176, North-Holland Publishing Co., Amsterdam, 1993.Google Scholar
[8] Diestel, J. and Uhl, J. J. Jr., Vector measures. Mathematical Surveys, 15, American Mathematical Society, Providence, RI, 1977.Google Scholar
[9] Harksen, J., Tensornormtopologien. Dissertation, Christian-Albrechts-Universität zu Kiel, 1979.Google Scholar
[10] Haydon, R., Levy, M., and Raynaud, Y., Randomly normed spaces. Travaux en Cours, 41, Hermann, Paris, 1991.Google Scholar
[11] Heinrich, S., Ultraproducts in Banach spaces theory. J. Reine Angew. Math. 313(1980), 72–104. doi:10.1515/crll.1980.313.72Google Scholar
[12] Lindenstrauss, J. and Tzafriri, L., Classical Banach spaces I. Sequence spaces. Ergebnisse der Mathematik und ihrer Grenzgebiete, 92, Springer-Verlag, Berlin-New York, 1977, and Classical Banach spaces II. Function spaces. Ergebnisse der Mathematik und ihrer Grenzgebiete, 97, Springer-Verlag, Berlin-New York, 1979.Google Scholar
[13] Lindenstrauss, J. and Tzafriri, L., The uniform approximation property in Orlicz spaces. Israel J. Math. 23(1976), no. 2, 142–155.Google Scholar
[14] Molina, J. A. López, Puerta, M. E., and Rivera, M. J., On the structure of ultraproducts of real interpolation spaces. Extracta Math. 16(2001), no. 3, 367–382. doi:10.1007/BF02756794Google Scholar
[15] Molina, J. A. López, Puerta, M. E., and Rivera, M. J., Ultraproducts of real interpolation spaces between Lp-spaces. Bull. Braz. Math. Soc. (N.S.) 37(2006), no. 2, 191–216. doi:10.1007/s00574-006-0010-5Google Scholar
[16] Molina, J. A. López and Pérez, E. A. Sánchez, On operator ideals related to (p, σ)-absolutely continuous operators. Studia Math. 138(2000), no. 1, 25–40.Google Scholar
[17] Matter, U., Factoring through interpolation spaces and super-reflexive Banach spaces. Rev. Roumaine Math. Pures Appl. 34(1989), no. 2, 147–156.Google Scholar
[18] Matter, U., Absolutely continuous operators and super-reflexivility. Dissertation, Universität Zürich, 1985.Google Scholar
[19] Puerta, M. E. and Loaiza, G., Sobre un ideal minimal de operadores definido a través de espacios de interpolación. Ingeniería y Ciencia 3(2007), no. 6, 63–89.Google Scholar
[20] Pelczyński, A. and Rosenthal, H. P., Localization techniques in Lp spaces. Studia Math. 52(1974/75), 263–289.Google Scholar
[21] Pietsch, A., Operator ideals. North-Holland Mathematical Library, 20, North-Holland Publishing Co., Amsterdam-New York, 1980.Google Scholar
[22] Rivera, M. J., On the classes of ℒ λ , quasi-ℒE and ℒλg spaces. Proc. Amer. Math. Soc. 133(2005), no. 7, 2035–2044. doi:10.1090/S0002-9939-05-07761-0Google Scholar
[23] Saphar, P., Produits tensoriels d’espaces de Banach et classes d’applications linéaires. Studia Math. 38(1970), 71–100.Google Scholar
[24] Sims, B., “Ultra”-techniques in Banach space theory. Queen's Papers in Pure and Applied Mathematics, 60, Queen's University, Kingston, ON, 1982.Google Scholar
[25] Tomášek, S., Projectively generated topologies on tensor products. Comment. Math. Univ. Carolinae 11(1979), no. 4, 745–768.Google Scholar