Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-18T10:03:48.803Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Linear Invariance of Lindelöf Numbers

Published online by Cambridge University Press:  20 November 2018

Jan Baars  and
Helma Gladdines
Jan Baars
Affiliation:
Faculteit der Wiskunde en Informatica, Vrije Universiteit, De Boelelaan 1081a, 1081 HV Amsterdam, The Netherlands
Helma Gladdines
Affiliation:
Faculteit der Wiskunde en Informatica, Vrije Universiteit, De Boelelaan 1081a, 1081 HV Amsterdam, The Netherlands
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X and Y be Tychonov spaces and suppose there exists a continuous linear bijection from Cp(X)to CP(Y). In this paper we develop a method that enables us to compare the Lindelöf number of Y with the Lindelöf number of some dense subset Z of X. As a corollary we get that if for perfect spaces X and Y, CP(X) and Cp(Y)are linearly homeomorphic, then the Lindelöf numbers of Jf and Fare equal. Another result in this paper is the following. Let X and Y be any two linearly ordered perfect Tychonov spaces such that Cp(X)and Cp(Y)are linearly homeomorphic. Let 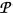be a topological property that is closed hereditary, closed under taking countable unions and closed under taking continuous images. Then X has isproperty 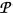if and only if Y has. As examples of such properties we consider certain cardinal functions.

Keywords

54C3557N17Function SpacesLindelöf Numbers
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 39 , Issue 2 , 01 June 1996 , pp. 129 - 137
Copyright
Copyright © Canadian Mathematical Society 1996

References

1. Arkhangel'skii, A. V., Cp-theory, In: Recent Progress in General Topology, (eds. J. van Mill and M. Husek), North Holland (1992), 1–56.Google Scholar
2. Arkhangel'skii, A. V., On linear homeomorphisms of function spaces, Soviet Math. Dokl. 25(1982), 852—855.Google Scholar
3. Arkhangel'ski, A. V., Problems in Cp-theory, In: Open Problems in Topology, (eds. J. van Mill and G. M. Reed), North Holland (1990), 601–616.Google Scholar
4. Arkhangel'ski, A. V., Topological function spaces, Kluwer Academic Publishers, Dordrecht, 1992.Google Scholar
5. Baars, J., Function spaces on first countable paracompact spaces, Bull. Pol. Acad. Sci. Math. 42(1994), 29–35.Google Scholar
6. Baars, J. and de Groot, J., On Topological and Linear Equivalence of certain Function Spaces, CWI-tract 86, Centre for Mathematics and Computer Science, Amsterdam.Google Scholar
7. Engelking, R., General Topology, Helderman Verlag, Berlin, 1989.Google Scholar
8. Juhâsz, I., Cardinal Functions II, Ten Years Later, MC Tract 123. Mathematical Centre, Amsterdam.Google Scholar
9. Okunev, O. G., A method for constructing examples of M-equivalent spaces, Top. and its Appl. 36(1990), 157–171.Google Scholar
10. Tkachuk, V. V., Duality with respect to the Cp-functor and cardinal invariants ofSouslin type, Mat. Zametki 37(1985), 441–450.Google Scholar