No CrossRef data available.
Article contents
On the ith Latent Root of a Complex Matrix(1)
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Goodman [1] has pointed out the applications of the distributional results of the complex multivariate normal statistical analysis. Khatri [4], has suggested the maximum latent root statistic for testing the reality of a covariance matrix. The joint distribution of the latent roots under certain null hypotheses can be written as, [2], [3],
1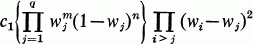
where
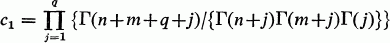
and
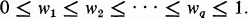
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1972
Footnotes
(2)
On leave.
(1)
This research was supported by the National Science Foundation Grant GP-7663.
References
1.
Goodman, N. R., Statistical analysis based on a certain multivariate complex Gaussion distribution (an introduction), Ann. Math. Stat. 34, (1963), 152-176.Google Scholar
2.
Khatri, C. G., Distribution of the largest or the smallest root under null hypotheses concerning complex multivariate normal, Ann. Math. Statist.
35 (1964), 1807-1810.Google Scholar
3.
Khatri, C. G., Classical statistical analysis based on a certain multivariate complex Gaussion distribution, Ann. Math. Statist. 36, (1965), 98-114.Google Scholar
4.
Khatri, C. G.,A test for reality of a covariance matrix in certain complex Gaussion distribution, Ann. Math. Statist. 36, (1965), 115-119.Google Scholar
5.
Pillai, K. C. S., and Dotson, C., Power comparisons of tests of two multivariate hypotheses based on individual characteristic roots, Mimeo. Series No. 108, Dept. of Statist., Purdue University, 1967.Google Scholar


