Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-30T21:47:56.989Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Inequality

Published online by Cambridge University Press:  20 November 2018

Peter Kardos
Peter Kardos*
Affiliation:
Physical Sciences Group, Scarborough College, University of Toronto, West Hill, Ontario, MIC 1A4
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we are concerned with the functional inequality

1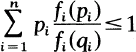

where 0 < Pi < l, 0 < qi < l, fi(p)≠0, for 0 < P < 1, (i = 1, 2,..., n) 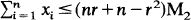and n is a fixed positive integer, n ≥ 2.

Inequality (1) was studied by Rényi and Fischer, (see [1], [3]) in the special case

2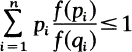

and this provided a characterization of Rényi's entropy.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 22 , Issue 4 , 01 December 1979 , pp. 483 - 489
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. Fischer, P., On the inequality Canadian Math. Bull. 17 (1974), 193-199.Google Scholar
2. Aczél, J. and Daróczy, Z., On Measures of Information and their Characterizations, Academic Press, New York, 1975.Google Scholar
3. Rényi, A., On the Foundations of Information Theory, Rev. Inst. Internat. Stat. 33 (1965), 1-14.Google Scholar
4. Aczél, J., General solution of an inequality containing several unknown functions, with applications to the generalized problem of how to keep the (inset) expert honest, Notices Amer. Math. Soc. vol. 25, nr. 4, p. A-435, #78T-C18.Google Scholar