No CrossRef data available.
Article contents
On the Image of Certain Extension Maps. I
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let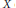 
$X$ be a smooth complex projective curve of genus 
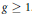$g\ge 1$. Let 
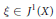$\xi \in {{J}^{1}}\left( X \right)$ be a line bundle on 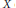$X$ of degree 1. Let 
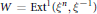$W=\text{Ex}{{\text{t}}^{1}}\left( {{\xi }^{n}},{{\xi }^{-1}} \right)$ be the space of extensions of 
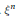${{\xi }^{n}}$ by 
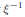${{\xi }^{-1}}$. There is a rational map 
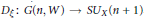${{D}_{\xi }}:G\left( n,W \right)\to S{{U}_{X}}\left( n+1 \right)$, where 
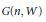$G\left( n,W \right)$ is the Grassmannian variety of 
$n$-linear subspaces of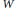 
$W$ and 
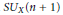$S{{U}_{X}}\left( n+1 \right)$ is the moduli space of rank 
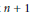$n+1$ semi-stable vector bundles on 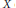$X$ with trivial determinant. We prove that if 
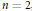$n=2$, then 
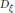${{D}_{\xi }}$ is everywhere defined and is injective.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2007
References
[1] Atiyah, M. F.. Complex analytic connections in fibre bundles. Trans. Amer. Math. Soc.
85(1957), 181–207.Google Scholar
[2] Brambila-Paz, L., Grzegorczyk, I., and Newstead, P. E., Geography of Brill-Noether loci for small slopes. J. Algebraic Geom.
6(1997), no. 4, 645–669.Google Scholar
[3] Benson, D. J.. Representations and Cohomology. I.
Second edition. Cambridge Studies in Advanced Mathematics 30, Cambridge University Press, Cambridge, 1998.Google Scholar
[4] Bertram, A., Moduli of rank-2 vector bundles, theta divisors, and the geometry of curves in projective space. J. Differential Geom.
35(1992), no. 2, 429–469.Google Scholar
[5] Lange, H. and Narasimhan, M. S.. Maximal subbundles of rank two vector bundles on curves. Math. Ann.
266(1983), no. 1, 55–72.Google Scholar
[6] Le Potier, J.. Lectures on Vector Bundles. Cambridge Studies in Advanced Mathematics 54, Cambridge University Press, Cambridge, 1997.Google Scholar
[7] Narasimhan, M. S. and Ramanan, S.. Moduli of vector bundles on a compact Riemann surface. Ann. of Math.
89(1969) 14–51.Google Scholar
[8] Narasimhan, M. S. and Seshadri, C. S., Stable and unitary vector bundles on a compact Riemann surface. Ann. of Math.
82(1965), 540–567.Google Scholar
[9] Seshadri, C. S., Space of unitary vector bundles on a compact Riemann surface. Ann. of Math.
85(1967), 303–336.Google Scholar
You have
Access