Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T15:04:55.767Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Extreme Points of Quotients of L∞ by Douglas Algebras

Published online by Cambridge University Press:  20 November 2018

Waleed Deeb  and
Rahman Younis
Waleed Deeb
Affiliation:
Kuwait University, Kuwait
Rahman Younis
Affiliation:
Kuwait University, Kuwait
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let B be a Douglas algebra which admits best approximation. It will be shown that the following are equivalent: (1) The unit ball of (L∞/B) has no extreme points; (2) For any Blaschke product b with 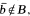, there exists h ∈ B such that 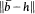= 1 and h|E≢0, where E is the essential set of B.

It will also be proven that if B⊇H∞+C and its essential set E contains a closed Gδ set, then the unit ball of (L∞/B) has no extreme points. Many known results concerning this subject will follow from these results.

Keywords

30H0546E1541A50
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 27 , Issue 4 , 01 December 1984 , pp. 517 - 522
Copyright
Copyright © Canadian Mathematical Society 1984

References

1. Axler, S., Berg, I., Jewell, N. and Shields, A., Approximation by compact operators and the space H∞+C, Annals of Math., 109(1979), 601-612.10.2307/1971228CrossRefGoogle Scholar
2. Clancey, K. F. and Gosselin, J. A., On the local theory of Toeplitz operators, Illinois J. Math. 22 (1978), 449-458.10.1215/ijm/1256048607CrossRefGoogle Scholar
3. Davie, A. M., Gamelin, T. W. and Garnett, J., Distance estimates and point-wise bounded density, Trans. Aoner. Math. Soc. 175(1973), 37-68.CrossRefGoogle Scholar
4. Gamelin, T. W., Uniform algebras, Prentice-Hall (1969).Google Scholar
5. Garnett, J., Bounded analytic functions, Academic Press (1981).Google Scholar
6. Gorkin, P., Decomposition of the maximal ideal space of L∞, Ph.D. -thesis, Michigan State University, 1982.Google Scholar
7. Hoffman, K., Banach spaces of analytic functions, Prentice-Hall (1962).Google Scholar
8. Izuchi, K. and Younis, R., On the quotient space of two Douglas algebras, submitted.Google Scholar
9. Izuchi, K., Extreme points of unit balls of quotients of L∞ by Douglas algebras, preprint.10.1215/ijm/1256044756CrossRefGoogle Scholar
10. Koosis, P., Weighted quadratic means of Hilbert transforms, Duke Math. J. 38 (1971), 609-634.10.1215/S0012-7094-71-03877-4CrossRefGoogle Scholar
11. Leucking, D. and Younis, R., Quotients of L∞ by Douglas algebras and Best approximation, Transaction, Amer. Math. Soc. V276(1983), 699-706.Google Scholar
12. Sarson, D., Function theory on the unit circle, Virginia Poly. Inst, and State Univ. (1979).Google Scholar
13. Sundberg, C., A note on algebras between L∞ and H∞ , Rocky Mount. J. Math. 11(1981), 333-336. 10.1216/RMJ-1981-11-2-333CrossRefGoogle Scholar
14. Younis, R., Best approximation in certain Douglas algebras, Proc. Amer. Math. Soc. 80 (1980), 639-642.10.1090/S0002-9939-1980-0587943-0CrossRefGoogle Scholar
15. Younis, R., Properties of certain algebras between L∞ and H∞, J. Funct. Anal. 44 (1981), 381-387.10.1016/0022-1236(81)90016-1CrossRefGoogle Scholar
16. Younis, R., M-ideals of L∞/H∞ and support sets, to appear in Illinois J. Math.Google Scholar