Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Clements, John
1974.
Existence Theorems for a Quasilinear Evolution Equation.
SIAM Journal on Applied Mathematics,
Vol. 26,
Issue. 4,
p.
745.
Ebihara, Yukiyoshi
1978.
On some nonlinear evolution equations with the strong dissipation.
Journal of Differential Equations,
Vol. 30,
Issue. 2,
p.
149.
Ebihara, Yukiyoshi
1979.
On some nonlinear evolution equations with the strong dissipation, II.
Journal of Differential Equations,
Vol. 34,
Issue. 3,
p.
339.
Pecher, Hartmut
1980.
On global regular solutions of third order partial differential equations.
Journal of Mathematical Analysis and Applications,
Vol. 73,
Issue. 1,
p.
278.
Yamada, Yoshio
1981.
Quasilinear wave equations and related nonlinear evolution equations.
Nagoya Mathematical Journal,
Vol. 84,
Issue. ,
p.
31.
Ebihara, Yukiyoshi
1982.
On some nonlinear evolution equations with strong dissipation, III.
Journal of Differential Equations,
Vol. 45,
Issue. 3,
p.
332.
Hai, Dang Dinh
1988.
On a quasilinear wave equation with nonlinear damping.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 110,
Issue. 3-4,
p.
227.
Ang, Dang Dinh
and
Pham Ngoc Dinh, A.
1988.
Strong Solutions of a Quasilinear Wave Equation with Nonlinear Damping.
SIAM Journal on Mathematical Analysis,
Vol. 19,
Issue. 2,
p.
337.
Dinh, A. Pham Ngoc
and
Ang, Dang Dinh
1989.
Nonlinear Hyperbolic Equations — Theory, Computation Methods, and Applications.
p.
499.
Hai, Dang Dinh
1991.
On a doubly damped quasilinear wave equation.
Annali di Matematica Pura ed Applicata,
Vol. 160,
Issue. 1,
p.
77.
Kawashima, S.
and
Shibata, Y.
1992.
Global existence and exponential stability of small solutions to nonlinear viscoelasticity.
Communications in Mathematical Physics,
Vol. 148,
Issue. 1,
p.
189.
Muñoz Rivera, Jaime E.
1995.
Existence and decay of weak solutions for systems arising in thermodynamics.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 24,
Issue. 6,
p.
825.
Zhijian, Yang
2002.
Blowup of solutions for a class of non‐linear evolution equations with non‐linear damping and source terms.
Mathematical Methods in the Applied Sciences,
Vol. 25,
Issue. 10,
p.
825.
Yacheng, Liu
and
Junsheng, Zhao
2004.
Multidimensional viscoelasticity equations with nonlinear damping and source terms.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 56,
Issue. 6,
p.
851.
Keyantuo, Valentin
and
Lizama, Carlos
2006.
Periodic solutions of second order differential equations in Banach spaces.
Mathematische Zeitschrift,
Vol. 253,
Issue. 3,
p.
489.
Benaissa, Abbès
and
Mokeddem, Soufiane
2007.
Decay estimates for the wave equation of p‐Laplacian type with dissipation of m‐Laplacian type.
Mathematical Methods in the Applied Sciences,
Vol. 30,
Issue. 2,
p.
237.
Kalantarov, Varga
and
Zelik, Sergey
2009.
Finite-dimensional attractors for the quasi-linear strongly-damped wave equation.
Journal of Differential Equations,
Vol. 247,
Issue. 4,
p.
1120.
Sun, Fuqin
Wang, Mingxin
and
Li, Huiling
2010.
Global and blow-up solutions for a quasilinear hyperbolic equation with strong damping.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 73,
Issue. 5,
p.
1408.
Liu, Xiaopan
and
Apreutesei, Narcisa C.
2012.
On Existence, Uniform Decay Rates, and Blow‐Up for Solutions of a Nonlinear Wave Equation with Dissipative and Source.
Abstract and Applied Analysis,
Vol. 2012,
Issue. 1,
Xu, Runzhang
Liu, Jie
Niu, Yi
and
Chen, Shaohua
2013.
Asymptotic behaviour of solution for multidimensional viscoelasticity equation with nonlinear source term.
Boundary Value Problems,
Vol. 2013,
Issue. 1,


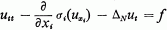
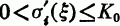 for some constant K
for some constant K