Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T21:55:27.440Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Endomorphism Rings of Local Cohomology Modules

Published online by Cambridge University Press:  20 November 2018

Kazem Khashyarmanesh
Kazem Khashyarmanesh*
Affiliation:
Ferdowsi University of Mashhad, Department of Mathematics, Mashhad, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

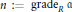Let $R$ be a commutative Noetherian ring and $\mathfrak{a}$ a proper ideal of $R$. We show that if $n\,:=\,\text{grad}{{\text{e}}_{R}}\,\mathfrak{a}$, then 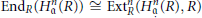$\text{En}{{\text{d}}_{R}}(H_{\mathfrak{a}}^{n}(R))\,\cong \,\text{Ext}_{R}^{n}(H_{\mathfrak{a}}^{n}(R),\,R)$. We also prove that, for a nonnegative integer $n$ such that 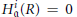$H_{\mathfrak{a}}^{i}(R)\,=\,0$ for every 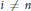$i\,\ne \,n$, if 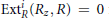$\text{Ext}_{R}^{i}({{R}_{z}},\,R)\,=\,0$ for all 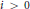$i\,>\,0$ and 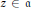$z\,\in \,\mathfrak{a}$, then 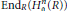$\text{En}{{\text{d}}_{R}}(H_{\mathfrak{a}}^{n}(R))$ is a homomorphic image of $R$, where 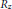${{R}_{z}}$ is the ring of fractions of $R$ with respect to a multiplicatively closed subset 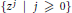$\{{{z}^{j}}|j\,\ge \text{0}\}$ of $R$. Moreover, if 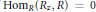$\text{Ho}{{\text{m}}_{R}}({{R}_{z}},R)=0$ for all 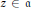$z\,\in \,\mathfrak{a}$, then 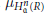${{\mu }_{H_{\mathfrak{a}}^{n}(R)}}$ is an isomorphism, where 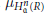${{\mu }_{H_{\mathfrak{a}}^{n}(R)}}$ is the canonical ring homomorphism 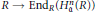$R\,\to \,\text{En}{{\text{d}}_{R}}(H_{\mathfrak{a}}^{n}(R))$.

Keywords

13D4513D0713D25local cohomology moduleendomorphism ringMatlis dual functorfilter regular sequence
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 53 , Issue 4 , 01 December 2010 , pp. 667 - 673
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Brodmann, M. and Sharp, R. Y., Local cohomology: an algebraic introduction with geometric applications. Cambridge Studies in Advanced Mathematics, 60, Cambridge University Press, Cambridge, 1998.Google Scholar
[2] Hellus, M., On the associated primes of Matlis duals of top local cohomology modules. Comm. Algebra 33(2005), no. 11, 3997–4009. doi:10.1080/00927870500261314Google Scholar
[3] Hellus, M., Finiteness properties of duals of local cohomology modules. Comm. Algebra 35(2007), no. 11, 3590–3602. doi:10.1080/00927870701512069Google Scholar
[4] Hellus, M. and Stückrad, J., Local Cohomology and Matlis duality. Univ. Iagel. Acta. Math. 45(2007), 63–70.Google Scholar
[5] Hellus, M. and Stückrad, J., On endomorphism rings of local cohomology. Proc. Amer. Math. Soc. 136(2008), no. 7, 2333–2341. doi:10.1090/S0002-9939-08-09240-XGoogle Scholar
[6] Khashyarmanesh, K., On the finiteness properties of extension and torsion functors of local cohomology modules. Proc. Amer. Math. Soc. 135(2007), no. 5, 1319–1327. doi:10.1090/S0002-9939-06-08664-3Google Scholar
[7] Khashyarmanesh, K., On the Matlis duals of local cohomology modules. 88(2007), no. 5, 413–418. doi:10.1007/s00013-006-1115-1Google Scholar
[8] Khashyarmanesh, K. and Salarian, Sh., Filter regular sequences and the finiteness of local cohomology modules. Comm. Algebra 26(1998), no. 8, 2483–2490. doi:10.1080/00927879808826293Google Scholar
[9] Lyubeznik, G., Finiteness properties of local cohomology modules (an application of D-modules to commutative algebra). Invent. Math. 113(1993), no. 1, 41–55. doi:10.1007/BF01244301Google Scholar
[10] Matlis, E., Injective modules over Noetherian rings. Pacific J. Math. 8(1958), 511–528.Google Scholar
[11] Schenzel, P., Trung, N. V., and Cuong, N. T., Verallgemeinerte Cohen-Macaulay-Moduln. Math. Nachr. 85(1978), 57–73. doi:10.1002/mana.19780850106Google Scholar
[12] Stückrad, J. and Vogel, W., Buchsbaum rings and applications. An interaction between algebra, geometry and topology. Springer-Verlag, Berlin, 1986.Google Scholar