No CrossRef data available.
Article contents
On the Dimension of an Irreducible Tensor Representation of the General Linear Group GL(d)
Published online by Cambridge University Press: 20 November 2018
Extract
As has long been known, the irreducible tensor representations of GL(d) of rank n may be labeled by means of the irreducible representations of Sn, i.e., by means of the Young diagrams [λ], where λ1 + λ2 + … λr = n. We denote such a tensor representation by 〈λ〉. Using Young's raising operator Rij we can write [1, p. 42]
1.1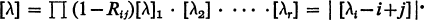
where the dot denotes the inducing process. For example, [3] . [2] is that representation of S5 induced by the identity representation of its subgroup S3 × S2.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1970


