Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T05:50:31.089Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Diameter of Unitary Cayley Graphs of Rings

Published online by Cambridge University Press:  20 November 2018

Huadong Su
Huadong Su*
Affiliation:
School of Mathematical and Statistics Sciences, Guangxi Teachers Education University, Nanning, Guangxi, 530023, P. R. China and Department of Mathematics and Statistics, Memorial University of Newfoundland, St.John's, Nfld A1C 5S7 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The unitary Cayley graph of a ring 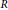$R$, denoted 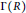$\Gamma \left( R \right)$, is the simple graph defined on all elements of 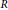$R$, and where two vertices $x$ and $y$ are adjacent if and only if 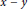$x\,-\,y$ is a unit in 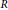$R$. The largest distance between all pairs of vertices of a graph 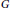$G$ is called the diameter of 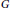$G$ and is denoted by 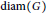$\text{diam}\left( G \right)$. It is proved that for each integer 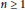$n\,\ge \,1$, there exists a ring 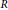$R$ such that 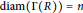$\text{diam}\left( \Gamma \left( R \right) \right)=n$. We also show that 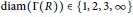$\text{diam}\left( \Gamma \left( R \right) \right)\in \left\{ 1,2,3,\infty \right\}$ for a ring 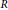$R$ with 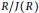${R}/{J\left( R \right)}\;$ self-injective and classify all those rings with 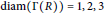$\text{diam}\left( \Gamma \left( R \right) \right)\,=\,1,\,2,\,3$, and 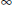$\infty$, respectively.

Keywords

05C2516U6005C12unitary Cayley graphdiameterk-goodunit sum numberself-injective ring
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 3 , 01 September 2016 , pp. 652 - 660
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Anderson, D. F. and Badawi, A., The total graph of a commutative ring. J. Algebra 320(2008), no. 7, 2706–2719. http://dx.doi.org/10.1016/j.jalgebra.2008.06.028 Google Scholar
[2] Akhtar, R., Jackson-Henderson, T., Karpman, R., Boggess, M., Jimenez, I., Kinzel, A., and Pritikin, D., On the unitary Cayley graph of a finite ring. Electron. J. Combin. 16(2009), no. 1, no. 117.Google Scholar
[3] Anderson, D. E. and Livingston, P. S., The zero-divisor graph of a commutative ring. J. Algebra 217(1999), no. 2, 434–447. http://dx.doi.org/10.1006/jabr.1 998.7840 Google Scholar
[4] Anderson, D. E. and Mulay, S. B., On the diameter and girth of a zero-divisor graph. J. Pure Appl. Algebra 210(2007), no. 2, 543–550. http://dx.doi.org/10.1 01 6/j.jpaa.2006.10.007 Google Scholar
[5] Ashrafi, N. and Vâmos, P., On the unit sum number of some rings. Q. J. Math. 56(2005), no. 1,1-12. http://dx.doi.org/1 0.1093/qmath/hah023 Google Scholar
[6] Berrizbeitia, P. and Giudici, R. E., Counting pure k-cycles in sequences of Cayley graphs.Discrete Math. 149(1996), no. 1-3, 11–18. http://dx.doi.org/10.101 6/0012-365X(94)00295-T Google Scholar
[7] Berrizbeitia, P. and Giudici, R. E., On cycles in the sequence of unitary Cayley graphs. Discrete Math. 282(2004), no. 1-3, 239–243. http://dx.doi.org/10.1016/j.disc.2003.11.013 Google Scholar
[8] Dejterand, I. J. and Giudici, R. E., On unitary Cayley graphs. J. Combin. Math.Combin.Comput. 18(1995), 121–124.Google Scholar
[9] DeMeyer, F. R., McKenzie, T., and Schneider, K., The zero-divisor graph of a commutative semigroup. Semigroup Forum 65(2002), no. 2, 206–214. http://dx.doi.org/10.1007/s002330010128 Google Scholar
[10] Fuchs, E. D., Longest induced cycles in circulant graphs.Electron. J. Combin. 12(2005), Research Paper 52.Google Scholar
[11] Henriksen, M., Two classes of rings generated by their units. J. Algebra 31(1974), 182–193. http://dx.doi.org/10.1016/0021-8693(74)90013-1 Google Scholar
[12] Heydari, F. and Nikmehr, M. J., The unit graph of a left Artinian ring.Acta Math.Hungar. 139(2013), no. 1-2, 134–146. http://dx.doi.org/10.1007/s10474-012-0250-3 Google Scholar
[13] Herwig, B. and Ziegler, M., A remark on sums of units.Arch. Math (Basel) 79(2002), no. 6, 430–431. http://dx.doi.org/10.1007/BF02638379 Google Scholar
[14] Ilic, A., The energy of unitary Cayley graphs. Linear Algebra Appl. 431(2009), no. 10,1881-1889. http://dx.doi.org/10.1016/j.laa.2009.06.025 Google Scholar
[15] Kiani, D. and Aghaei, M. M. H., On the unitary Cayley graph of a ring. Electron. J. Combin. 19(2012), no. 2, no. 10.Google Scholar
[16] Kiani, D., Aghaei, M. M. H., Meemark, Y., and Suntornpoch, B., Energy of unitary Cayley graphs and gcd-graphs. Linear Algebra Appl. 435(2011), no. 6,1336-1343. http://dx.doi.org/1 0.101 6/j.laa.2O11.03.01 5 Google Scholar
[17] Klotz, W. and Sander, T., Some properties of unitary Cayley graphs.Electron. J. Combin. 14(2007), 45.Google Scholar
[18] Khurana, D. and Srivastava, A. K., Unit sum numbers of right self-injective rings. Bull. Austral. Math. Soc. 75(2007), no. 3, 355–360. http://dx.doi.org/10.101 7/S0004972700039289 Google Scholar
[19] Lucchini, A. and Maroti, A., Some results and questions related to the generating graph of a finite group.In: Ischia group theory 2008, World Sci. Publ., Hackensack, NJ, 2009, pp. 183–208. http://dx.doi.org/10.1142/9789814277808J3014 Google Scholar
[20] Lanski, C. and Maroti, A., Ring elements as sums of units.Cent. Eur. J. Math. 7(2009), no. 3, 395–399. http://dx.doi.org/!0.2478/s!1533-009-0024-5 Google Scholar
[21] Liu, X. and Zhou, S., Spectral properties of unitary Cayley graphs of finite commutative rings. Electron. J. Combin. 19(2012), no. 13.Google Scholar
[22] Vâmos, P., 2-good rings. Q. J. Math. 56(2005), no. 3, 417–430. http://dx.doi.org/10.1093/qmath/hahO46 Google Scholar
[23] Wolfson, K. G., An ideal theoretic characterization of the ring of all linear transformations.Amer. J. Math. 75(1953), 358–386. http://dx.doi.org/10.2307/2372458 Google Scholar
[24] Zelinsky, D., Every linear transformation is sum of nonsingular ones. Proc. Amer. Math. Soc. 5(1954), 627–630. http://dx.doi.org/10.1090/S0002-9939-1954-0062728-7 Google Scholar