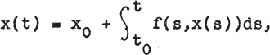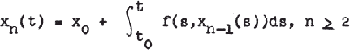Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Dinghas, Alexander
1958.
Zur Existenz von Fixpunkten bei Abbildungen vom Abel-Liouvilleschen Typus.
Mathematische Zeitschrift,
Vol. 70,
Issue. 1,
p.
174.
Luxemburg, W.A.J.
1958.
On the convergence of successive approximations in the theory of ordinary differential equations, II.
Indagationes Mathematicae (Proceedings),
Vol. 61,
Issue. ,
p.
540.
Brauer, Fred
1959.
Some Results on Uniqueness and Successive Approximations.
Canadian Journal of Mathematics,
Vol. 11,
Issue. ,
p.
527.
Walter, Wolfgang
1964.
Bemerkungen zu verschiedenen Eindeutigkeitskriterien f�r gew�hnliche Differentialgleichungen.
Mathematische Zeitschrift,
Vol. 84,
Issue. 3,
p.
222.
Ziebur, A. D.
1965.
Uniqueness and the convergence of successive approximations. II.
Proceedings of the American Mathematical Society,
Vol. 16,
Issue. 3,
p.
335.
1969.
Differential and Integral Inequalities - Theory and Applications: Ordinary Differential Equations.
Vol. 55,
Issue. ,
p.
355.
1970.
Iterative Solution of Nonlinear Equations in Several Variables.
p.
523.
Müller, G.O
1982.
Continuity moduli criteria for ODE's in a Banach space.
Journal of Differential Equations,
Vol. 45,
Issue. 3,
p.
317.
Filip, Alexandru-Darius
and
Petruşel, Adrian
2015.
Fixed point theorems for operators in generalized Kasahara spaces.
Revista de la Real Academia de Ciencias Exactas, Fisicas y Naturales. Serie A. Matematicas,
Vol. 109,
Issue. 1,
p.
15.
Arutyunov, Aram V.
and
Zhukovskiy, Sergey E.
2017.
Covering mappings and their applications.
p.
1.
Alshybani, Shaymaa
Mansour Vaezpour, S
and
Jaafar Mahmood, Sahar
2019.
Generalized Hyers-Ulam Stability Of Mixed Type Additive-Quadratic Functional Equation Of Random Homomorphisms In Random Normed Algebras.
Journal of Physics: Conference Series,
Vol. 1294,
Issue. 3,
p.
032004.
Cobzaş, S.
2022.
Compact bilinear operators on asymmetric normed spaces.
Topology and its Applications,
Vol. 306,
Issue. ,
p.
107922.
Boonsri, Narongsuk
and
Saejung, Satit
2024.
On contraction principles for mappings defined on a metric space with a directed graph.
Journal of Mathematical Analysis and Applications,
Vol. 530,
Issue. 1,
p.
127656.
Benhammouda, Brahim
and
Vazquez-Leal, Hector
2025.
Exploring a Novel Multi-Stage Differential Transform Method Coupled with Adomian Polynomials for Solving Implicit Nonlinear ODEs with Analytical Solutions.
Mathematics,
Vol. 13,
Issue. 3,
p.
358.