Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2025-01-02T17:59:54.969Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Closure of the Convex Hull of a Set

Published online by Cambridge University Press:  20 November 2018

C.-S. Lin
C.-S. Lin*
Affiliation:
University of New Brunswick Fredericton, N.B., Canada
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Y be a linear space over the complex plane C, and let F be a mapping on the complex linear space Y ⊕ C into subsets of C with the following properties: for y ∊ Y, λ and μ ∊ C, F(y + μ) is a nonempty and bounded subset of C, F(λy + μ) = λF(y) + μ and F(μ) = {μ}. We shall write f(y + μ) = sup{|λ + μ|: λ ∊ F(y)}, the radius of F(y + μ), y ∊ Y and μ ∊ C. The convex hull (resp. the closure) of a subset M of C is denoted by conv M (resp. ).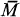

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 18 , Issue 1 , April 1975 , pp. 147 - 148
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Furata, T. and Nakamoto, R., On the numerical range of an operator, Proc. Japan Acad. 47 (1971), 279-284.Google Scholar
2. Nieto, J. I., On Fredholm operators and the essential spectrum of singular integral operators, Math. Ann. 178 (1968), 62-77.Google Scholar
3. Stampfli, J. G. and Williams, J. P., Growth conditions and the numerical range in a Banach algebra, Tôhoku Math. J. 20 (1968), 417-424.Google Scholar