Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2025-01-01T09:56:50.289Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Bound of the C* Exponential Length

Published online by Cambridge University Press:  20 November 2018

Qingfei Pan  and
Kun Wang
Qingfei Pan
Affiliation:
School of Mechanical and Electrical Engineering, Sanming University, Sanming, Fujian, China e-mail: [email protected]
Kun Wang
Affiliation:
Department of Mathematics, University of Puerto Rico, Rio Piedras Campus, San Juan, Puerto Rico, USA 00931 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 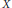$X$ be a compact Hausdorff space. In this paper, we give an example to show that there is 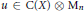$u\,\in \,C\left( X \right)\,\otimes \,{{M}_{n}}$ with 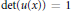$\det \left( u\left( x \right) \right)\,=\,1$ for all 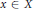$x\,\in \,X$ and 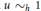$u{{\tilde{\ }}_{h}}1$ such that the 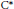${{C}^{*}}$ exponential length of $u$ (denoted by 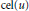$\text{cel}\left( u \right)$) cannot be controlled by $\pi$. Moreover, in simple inductive limit 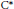${{C}^{*}}$-algebras, similar examples also exist.

Keywords

46L05exponential length
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 4 , 01 December 2014 , pp. 853 - 869
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Bhatia, R. and Davis, C., A bound for the spectral variation of a unitary operator.Linear and Multilinear Algebra 15 (1984), no. 1, 71–76. http://dx.doi.org/10.1080/03081088408817578 Google Scholar
[2] Choi, M. D. and Elliott, G. A., Density of the self-adjoint elements with finite spectrum in an irrational rotation C*-algebra.Math. Scand. 67 (1990), no. 1, 73–86.Google Scholar
[3] Elliott, G. A., Gong, G., and Li, L., On the classification of simple inductive limit C*-algebras. II. The isomorphism theorem. Invent. Math. 168 (2007) no. 2, 249–320. http://dx.doi.org/10.1007/s00222-006-0033-y Google Scholar
[4] Gong, G. and Lin, H., The exponential rank of inductive limit C*-algebras. Math. Scand. 71 (1992), no. 2, 301–319.Google Scholar
[5] Goodearl, K. R., Notes on a class of simple C*-algebras with real rank zero.Publ. Mat. 36 (1992), no. 2A, 637–654. http://dx.doi.org/10.5565/PUBLMAT 362A92 23 Google Scholar
[6] Guillemin, V. and Pollack, A., Differential topology. Prentice-Hall, Inc., Englewood Cliffs, NJ, 1974.Google Scholar
[7] Kadison, R. V. and Ringrose, J. R., Fundamentals of the theory of operator algebras, Vol. 1, Elementary theory. Pure and Applied Mathematics, Academic Press, New York, 1983.Google Scholar
[8] Lin, H., Exponential rank of C*-algebras with real rank zero and Brown-Pedersen conjectures. J. Funct. Anal. 114 (1993) no. 1, 1–11. http://dx.doi.org/10.1006/jfan.1993.1060 Google Scholar
[9] Lin, H., Exponentials in simple Z-stable C*-algebras.J. Funct. Anal., 266 (2014), no. 2, 754–791. http://dx.doi.org/10.1016/j.jfa.2013.09.023 Google Scholar
[10] Lin, H., Generalized Weyl-von Neumann theorems.Internat. J. Math. 2 (1991), no. 6, 725–739. http://dx.doi.org/10.1142/S0129167X91000405 Google Scholar
[11] Lin, H., Generalized Weyl-von Neumann theorems. II.Math. Scand. 77 (1995), no. 1, 129–147.Google Scholar
[12] Lin, H., Simple nuclear C*-algebras of tracial topological rank one.J. Funct. Anal. 251 (2007), no. 2, 601–679. http://dx.doi.org/10.1016/j.jfa.2007.06.016 Google Scholar
[13] Phillips, N. C., Simple C*-algebras with the property weak (FU).Math. Scand. 69 (1991), no. 1, 127–151.Google Scholar
[14] Phillips, N. C., How many exponentials? Amer. J. Math. 116 (1994), no. 6, 1513–1543. http://dx.doi.org/10.2307/2375057 Google Scholar
[15] Phillips, N. C., Reduction of exponential rank in direct limits of C*-algebras.Canad. J. Math. 46 (1994), no. 4, 818–853. http://dx.doi.org/10.4153/CJM-1994-047-7 Google Scholar
[16] Phillips, N. C., Approximation by unitaries with finite spectrum in purely infinite C*-algebras.J. Funct. Anal. 120 (1994), no. 1, 98–106. http://dx.doi.org/10.1006/jfan.1994.1025 Google Scholar
[17] Phillips, N. C., Exponential length and traces.Proc. Roy. Soc. Edinburgh Sect. A 125 (1995), no. 1, 13–29. http://dx.doi.org/10.1017/S0308210500030730 Google Scholar
[18] Phillips, N. C. and Ringrose, J. R., Exponential rank in operator algebras. In: Current topics in operator algebras (Nara, 1990),World Sci. Publ., River Edge, NJ, 1991, pp. 395–413.Google Scholar
[19] Ringrose, J. R., Exponential length and exponential rank in C*-algebras.Proc. Roy. Soc. Edinburgh Sect. A 121 (1992), no. 1–2, 55–71. http://dx.doi.org/10.1017/S0308210500014141 Google Scholar
[20] Thomsen, K., Homomorphisms between finite direct sums of circle algebra.Linear and Multilinear Algebra 32 (1992), 33–50. http://dx.doi.org/10.1080/03081089208818145 Google Scholar
[21] Thomsen, K., On the reduced C*-exponential length. In: Operator algebras and quantum field theory (Rome, 1996), Int. Press, Cambridge, MA, 1997, pp. 59–64.Google Scholar
[22] Weyl, H., Das asymptotische Verteilungsgesetz der Eigenwerte linearer partieller Differentialgleichungen.Math. Ann. 71 (1912), no. 4, 441–479. http://dx.doi.org/10.1007/BF01456804 Google Scholar
[23] Zhang, S., On the exponential rank and exponential length of C*-algebras.J. Operator Theory 28 (1992), no. 2, 337–355.Google Scholar
[24] Zhang, S., Exponential rank and exponential length of operators on Hilbert C*-algebras.Ann. of Math. 137 (1993), no. 1, 129–144. http://dx.doi.org/10.2307/2946620 Google Scholar
[25] Zhang, S., Factorizations of invertible operators and K-theory of C*-algebras.Bull. Amer. Math. Soc. 28 (1993), no. 1, 75–83. http://dx.doi.org/10.1090/S0273-0979-1993-00334-3 Google Scholar