No CrossRef data available.
Article contents
On the binomial transforms of Apéry-like sequences
Published online by Cambridge University Press: 08 January 2025
Abstract
In his proof of the irrationality of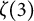 
$\zeta (3)$ and 
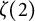$\zeta (2)$, Apéry defined two integer sequences through 
$3$-term recurrences, which are known as the famous Apéry numbers. Zagier, Almkvist–Zudilin, and Cooper successively introduced the other 
$13$ sporadic sequences through variants of Apéry’s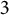 
$3$-term recurrences. All of the 
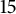$15$ sporadic sequences are called Apéry-like sequences. Motivated by Gessel’s congruences mod 
$24$ for the Apéry numbers, we investigate congruences of the form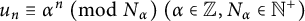 
$u_n\equiv \alpha ^n \ \pmod {N_{\alpha }}~(\alpha \in \mathbb {Z},N_{\alpha }\in \mathbb {N}^{+})$ for all of the 
$15$ Apéry-like sequences 
$\{u_n\}_{n\ge 0}$. Let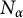 
$N_{\alpha }$ be the largest positive integer such that 
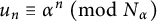$u_n\equiv \alpha ^n\ \pmod {N_{\alpha }}$ for all non-negative integers n. We determine the values of 
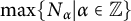$\max \{N_{\alpha }|\alpha \in \mathbb {Z}\}$ for all of the 
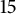$15$ Apéry-like sequences 
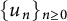$\{u_n\}_{n\ge 0}$. The binomial transforms of Apéry-like sequences provide us a unified approach to this type of congruences for Apéry-like sequences.
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society
Footnotes
This work was supported by the National Natural Science Foundation of China (Grant No. 12171370).
References
Almkvist, G. and Zudilin, W.,
Differential equations, mirror maps and zeta values
. In: N. Yui, S.-T. Yau, and J. D. Lewis (eds.), Mirror symmetry. V, AMS/IP Studies in Advanced Mathematics, 38, American Mathematical Society, Providence, RI, 2006, pp. 481–515.Google Scholar
Beukers, F.,
$p$
-linear schemes for sequences modulo
${p}^r$
. Indag. Math. (N.S.) 35(2024), 698–707.CrossRefGoogle Scholar
$p$
-linear schemes for sequences modulo
${p}^r$
. Indag. Math. (N.S.) 35(2024), 698–707.CrossRefGoogle ScholarBostan, A., Straub, A. and Yurkevich, S.,
On the representability of sequences as constant terms
. J. Number Theory 253(2023), 235–256.CrossRefGoogle Scholar
Chowla, S., Cowles, J. and Cowles, M.,
Congruence properties of Apéry numbers
. J. Number Theory 12(1980), 188–190.CrossRefGoogle Scholar
Cooper, S.,
Sporadic sequences, modular forms and new series for
$1/\pi$
. Ramanujan J. 29(2012), 163–183.CrossRefGoogle Scholar
$1/\pi$
. Ramanujan J. 29(2012), 163–183.CrossRefGoogle ScholarDenef, J. and Lipshitz, L.,
Algebraic power series and diagonals
. J. Number Theory 26(1987), 46–67.CrossRefGoogle Scholar
Gessel, I.,
Some congruences for Apéry numbers
. J. Number Theory 14(1982), 362–368.CrossRefGoogle Scholar
Gorodetsky, O.,
New representations for all sporadic Apéry-like sequences, with applications to congruences
. Exp. Math. 32(2023), 641–656.CrossRefGoogle Scholar
Kazandzidis, G.S.,
Congruences on the binomial coefficients
. Bull. Soc. Math. Grèce (N.S.) 9(1968), 1–12.Google Scholar
Malik, A. and Straub, A.,
Divisibility properties of sporadic Apéry-like numbers
. Res. Number Theory 2(2016), 5.CrossRefGoogle Scholar
Rowland, E. and Yassawi, R.,
Automatic congruences for diagonals of rational functions
. J. Théor. Nombres Bordx. 27(2015), 245–288.CrossRefGoogle Scholar
Straub, A.,
On congruence schemes for constant terms and their applications
. Res. Number Theory 8(2022), 42.CrossRefGoogle Scholar
Zagier, D.,
Integral solutions of Apéry-like recurrence equations
. In: J. Harnad and P. Winternitz (eds.), Groups and Symmetries, CRM Proceedings and Lecture Notes, 47, American Mathematical Society, Providence, RI, 2009, pp. 349–366.CrossRefGoogle Scholar