Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-29T03:31:31.336Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Bezdek–Pach Conjecture for Centrally Symmetric Convex Bodies

Published online by Cambridge University Press:  20 November 2018

Zsolt Lángi  and
Márton Naszódi
Zsolt Lángi
Affiliation:
Department of Geometry, BudapestUniversity of Technology, Budapest, Egry József u. 1., Hungary, 1111 e-mail: [email protected]
Márton Naszódi
Affiliation:
Department of Math. and Statistics, University of Alberta, Edmonton, AB, T6G 2G1 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Bezdek–Pach conjecture asserts that the maximum number of pairwise touching positive homothetic copies of a convex body in 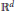${{\mathbb{R}}^{d}}$ is 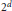${{2}^{d}}$. Naszódi proved that the quantity in question is not larger than 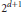${{2}^{d+1}}$. We present an improvement to this result by proving the upper bound 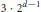$3\,\cdot \,{{2}^{d-1}}$ for centrally symmetric bodies. Bezdek and Brass introduced the one-sided Hadwiger number of a convex body. We extend this definition, prove an upper bound on the resulting quantity, and show a connection with the problem of touching homothetic bodies.

Keywords

52C1751N2051K0552A2152A37Bezdek–Pach conjecturehomothetspackingHadwiger numberantipodality
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 52 , Issue 3 , 01 September 2009 , pp. 407 - 415
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Bezdek, K. and Brass, P., On k + -neighbour packings and one-sided Hadwiger configurations. Beiträge Algebra Geom. 44(2003), no. 2, 493–498.Google Scholar
[2] Bezdek, K. and Connelly, R., Intersection points. Ann. Univ. Sci. Budapest. Eötvös Sect. Math. 31(1988), 115–127.Google Scholar
[3] Böröczky, K. Jr., Finite Packing and Covering, Cambridge Tracts in Mathematics 15, Cambridge University Press, Cambridge, 2004.Google Scholar
[4] Danzer, L. and Grünbaum, B., Über zwei Probleme bezüglich konvexer Körper von P. Erdʺos und von V. L. Klee. Math. Z. 79(1962), 95–99.Google Scholar
[5] Tóth, L. Fejes, Ü ber eine affininvariante Maßzahl bei Eipolyedern. Studia Sci.Math. Hungar. 5(1970), 173–180.Google Scholar
[6] Hadwiger, H., Über Treffanzahlen bei translationsgleichen Eikörpern. Arch. Math. 8(1957), 212–213.Google Scholar
[7] Naszódi, M., On a conjecture of Károly Bezdek and János Pach, Period. Math. Hungar. 53(2006), no. 1-2, 227–230.Google Scholar
[8] Petty, C. M., Equilateral sets in Minkowski spaces. Proc. Amer. Math. Soc. 29(1971), 369–374.Google Scholar