Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-02-11T12:37:14.515Z Has data issue: false hasContentIssue false
  • English
  • Français

On the average value of 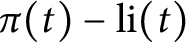$\pi (t)-\operatorname {\textrm {li}}(t)$

Part of: Zeta and $L$-functions: analytic theory Multiplicative number theory

Published online by Cambridge University Press:  14 March 2022

Daniel R. Johnston Open the ORCID record for Daniel R. Johnston [Opens in a new window]
Daniel R. Johnston*
Affiliation:
School of Science, The University of New South Wales Canberra, Northcott Drive, Campbell, ACT 2612, Australia
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that the Riemann hypothesis is equivalent to the condition 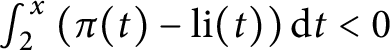$\int _{2}^x\left (\pi (t)-\operatorname {\textrm {li}}(t)\right )\textrm {d}t<0$ for all 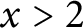$x>2$ . Here, 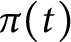$\pi (t)$ is the prime-counting function and 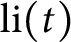$\operatorname {\textrm {li}}(t)$ is the logarithmic integral. This makes explicit a claim of Pintz. Moreover, we prove an analogous result for the Chebyshev function 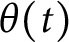$\theta (t)$ and discuss the extent to which one can make related claims unconditionally.

Keywords

Distribution of primesprime-counting functionlogarithmic integralRiemann hypothesisRiemann zeta function

MSC classification

Primary: 11M26: Nonreal zeros of $zeta (s)$ and $L(s, chi)$; Riemann and other hypotheses
Secondary: 11N05: Distribution of primes
Type
Article
Information
Canadian Mathematical Bulletin , Volume 66 , Issue 1 , March 2023 , pp. 185 - 195
Check for updates
Copyright
© Canadian Mathematical Society, 2022

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bays, C. and Hudson, R. H., A new bound for the smallest x with $\pi (x)>\textsf{li}(x)$ . Math. Comp. 69(2000), 1285–1296.CrossRefGoogle Scholar
Bennett, M., Martin, G., O’Bryant, K., and Rechnitzer, A., Explicit bounds for primes in arithmetic progressions . Illinois J. Math. 62(2018), nos. 1–4, 427–532.CrossRefGoogle Scholar
Brent, R., Platt, D., and Trudgian, T., Accurate estimation of sums over zeros of the Riemann zeta-function . Math. Comp. 90(2021), 2923–2935.CrossRefGoogle Scholar
Broughan, K., Equivalents of the Riemann hypothesis. Volume 1: arithmetic equivalents, Cambridge University Press, Cambridge, 2017.Google Scholar
Büthe, J., On the first sign change in Mertens’ theorem . Acta Arith. 171(2015), no. 2, 183–195.CrossRefGoogle Scholar
Büthe, J., An analytic method for bounding $\psi (x)$ . Math. Comp. 87(2018), no. 312, 1991–2009.CrossRefGoogle Scholar
Edwards, H. M., Riemann’s zeta function, Dover Publications, New York, 1974.Google Scholar
Ford, K., Zero-free regions for the Riemann zeta function . In: Number theory for the millennium, II (Urbana, IL, 2000), A K Peters, Natick, MA, 2002, pp. 25–56.Google Scholar
Garcia, S. R. and Lee, E. S., Unconditional explicit Mertens’ theorems for number fields and Dedekind zeta residue bounds . Ramanujan J. 57(2022), no. 3, 1169–1191.CrossRefGoogle Scholar
Granville, A. and Martin, G., Prime number races . Amer. Math. Monthly 113(2006), no. 1, 1–33.CrossRefGoogle Scholar
Humphries, P., The distribution of weighted sums of the Liouville function and Pólya’s conjecture . J. Number Theory 133(2013), no. 2, 545–582.CrossRefGoogle Scholar
Ingham, A. E., The distribution of prime numbers, Cambridge University Press, New York, 1964.Google Scholar
Kaczorowski, J., On sign-changes in the remainder-term of the prime number formula, I . Acta Arith. 44(1984), 365–377.CrossRefGoogle Scholar
Karatsuba, A. A., On the Riemann asymptotic formula for $\pi (x)$ . Dokl. Math. 69(2004), no. 3, 423–424.Google Scholar
Lamzouri, Y., A bias in Mertens’ product formula . Int. J. Number Theory 12(2016), no. 1, 97–109.CrossRefGoogle Scholar
Littlewood, J. E., Sur la distribution des nombres premiers . CR Acad. Sci. Paris 158(1914), no. 1914, 1869–1872.Google Scholar
Martin, G., Mossinghoff, M. J., and Trudgian, T. S., Fake mu’s. Preprint, 2021. arXiv:2112.05227CrossRefGoogle Scholar
Mossinghoff, M. J. and Trudgian, T. S., Nonnegative trigonometric polynomials and a zero-free region for the Riemann zeta-function . J. Number Theory 157(2015), 329–349.CrossRefGoogle Scholar
Pintz, J., On an assertion of Riemann concerning the distribution of prime numbers . Acta Math. Hungar. 58(1991), nos. 3–4, 383–387.CrossRefGoogle Scholar
Platt, D. J. and Trudgian, T. S., On the first sign change of $\theta (x)-x$ . Math. Comp. 85(2016), no. 299, 1539–1547.CrossRefGoogle Scholar
Riemann, B., Ueber die Anzahl der Primzahlen unter einer gegebenen Grosse . Ges. Math. Werke und Wissenschaftlicher Nachlaß. 2(1859), 145–155.Google Scholar
Rosser, J. B. and Schoenfeld, L., Approximate formulas for some functions of prime numbers . Illinois J. Math. 6(1962), no. 1, 64–94.CrossRefGoogle Scholar
Rubinstein, M. and Sarnak, P., Chebyshev’s bias . Exp. Math. 3(1994), no. 3, 173–197.CrossRefGoogle Scholar
Saouter, Y., Trudgian, T., and Demichel, P., A still sharper region where $\pi (x)- li(x)$ is positive. Math. Comp. 84(2015), no. 295, 2433–2446.Google Scholar
Schmidt, E., Über die Anzahl der Primzahlen unter gegebener Grenze . Math. Ann. 57(1903), no. 2, 195–204.CrossRefGoogle Scholar
Stechkin, S. B. and Popov, A. Y., The asymptotic distribution of prime numbers on the average . Russian Math. Surveys 51(1996), 6.CrossRefGoogle Scholar