Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T02:23:21.483Z Has data issue: false hasContentIssue false
  • English
  • Français

On Sturm's Separation Theorem

Published online by Cambridge University Press:  20 November 2018

Paul R. Beesack
Paul R. Beesack*
Affiliation:
Carleton University, Ottawa, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The purpose of this note is to obtain an extension of the classical Sturm separation theorem for the second order, linear selfadjoint differential equation

1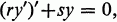

to the case of a noncompact interval. The classical theorem (cf. [3, p. 209], [4, p. 224]) assumes that r and s are continuous with r positive on a compact interval I, and concludes that between each pair of zeros (on I) of one (nontrivial) solution of (1) there lies precisely one zero of any other linearly independent solution of (1). If I is not compact, a function y which is a solution of (1) on /may often be extended (continuously) to an endpoint, say a, of I.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 15 , Issue 4 , December 1972 , pp. 481 - 487
Copyright
Copyright © Canadian Mathematical Society 1972

References

1. Beesack, P. R., Integral inequalities of the Wirtinger type, Duke Math. J. 25 (1958), 477-498.Google Scholar
2. Beesack, P. R., Integral inequalities involving a function and its derivative, Amer. Math. Monthly 78(1971), 705-741.Google Scholar
3. Coddington, E. A. and Levinson, N., Theory of ordinary differential equations, New York, 1955.Google Scholar
4. Ince, E. L., Ordinary differential equations, (reprint), Dover, New York, 1944.Google Scholar