Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T16:53:40.568Z Has data issue: false hasContentIssue false
  • English
  • Français

On Some Special Factorizations of (1-xn)/(1-x)

Published online by Cambridge University Press:  20 November 2018

L. Carlitz  and
L. Moser
L. Carlitz
Affiliation:
Duke University, Durham, North Carolina and University of Alberta, Edmonton, Alberta
L. Moser
Affiliation:
Duke University, Durham, North Carolina and University of Alberta, Edmonton, Alberta
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A: a1 < a2 < … < ak be a set of non-negative integers We call the corresponding polynomial 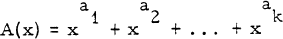the characteristic polynomial, or briefly, the c-polynomial of A. Any polynomial of such a form we call a c-polynomial and any factorization of a c-polynomial into others of the kind we call a c-factorization. If a c-polynomial cannot be factored in this way we call it c-irreducible. In this note we will determine all c-factorizations of the polynomial 1 + x + x2 + … + xn-1, and will find under what circumstances the c-irreducible factors are also irreducible in the usual sense, i.e., irreducible over the field of rationals.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 9 , Issue 4 , October 1966 , pp. 421 - 426
Copyright
Copyright © Canadian Mathematical Society 1966

References

1. De Bruijn, N. G., On number systems, Nieuw Archief voor Wiskunde (3), 4, (1956), pages 15-17.Google Scholar
2. Carlitz, L., Eulerian numbers and polynomials. Mathematics Magazine, 32, (1958), pages 247-258.Google Scholar