On Some Properties of Functions Regular in the Unit Circle

Extract

The space H_p, 1 ≤ p ≤ ∞ consists of those analytic functions f(z) regular in the unit circle, for which M_p (f;r) is bounded for O ≤ r ≤ 1, where

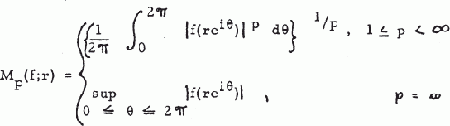
These spaces have been extensively studied.

One well known result concerning these spaces is that if f(z) = Σ ^∞_n=0 a_nzⁿ and {a_n} ɛ l_p for some p, 1 ≤ p ≤ 2, then f ɛ H_q, where p^-1+q^-1 = 1, and conversely if f ɛ H_p, 1 ≤ p ≤ 2, then {a_n} ɛ l_q. We propose to generalize this result to deal with functions f(z) = Σ ^∞_n=0 a_nzⁿ with {n^-λ a_n; n = 1, 2,...} ɛ l_p, where λ ≥ 0. The resulting generalization is contained in the theorems below.

However, in order to make these generalizations we must first generalize the spaces H_p. To this end we make the following definition.