Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Erdős, P.
Graham, R. L.
Ruzsa, I. Z.
and
Straus, E. G.
1975.
On the prime factors of (²ⁿ_{𝑛}).
Mathematics of Computation,
Vol. 29,
Issue. 129,
p.
83.
Bang, Thøger
and
Fuglede, Bent
1990.
No two quotients of normalized binomial mid-coefficients are equal.
Journal of Number Theory,
Vol. 35,
Issue. 3,
p.
345.
Moshe, Yossi
2004.
On a problem of Granville and Zhu Regarding Pascal's triangle.
Mathematika,
Vol. 51,
Issue. 1-2,
p.
63.
Moshe, Yossi
2007.
On subword decomposition and balanced polynomials.
Journal of Number Theory,
Vol. 123,
Issue. 1,
p.
224.
SHEVELEV, VLADIMIR
2007.
ON DIVISIBILITY OF ${\fontsize{9}{11}\selectfont\Big(\!\!\begin{array}{c}n-i-1\\[2pt]i-1\end{array}\!\!\Big)}$ by i.
International Journal of Number Theory,
Vol. 03,
Issue. 01,
p.
119.
Akiyama, Shigeki
2014.
Mean divisibility of multinomial coefficients.
Journal of Number Theory,
Vol. 136,
Issue. ,
p.
438.


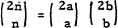
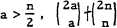 , which by the fact that there is a prime p satisfying n < p ≤ 2n immediately implies that
, which by the fact that there is a prime p satisfying n < p ≤ 2n immediately implies that