Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-24T06:14:26.210Z Has data issue: false hasContentIssue false
  • English
  • Français

On Single-Distance Graphs on the Rational Points in Euclidean Spaces

Part of: Elementary number theory Graph theory

Published online by Cambridge University Press:  29 July 2020

Sheng Bau ,
Peter Johnson  and
Matt Noble
Sheng Bau
Affiliation:
School of Mathematics, Statistics and Computer Science, University of Kwazulu-Natal, Durban, South Africa e-mail: [email protected]
Peter Johnson
Affiliation:
Department of Mathematics and Statistics, Auburn University, Auburn, Alabama e-mail: [email protected]
Matt Noble*
Affiliation:
Department of Mathematics and Statistics, Middle Georgia State University, Macon, Georgia
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For positive integers n and d > 0, let 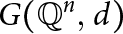$G(\mathbb {Q}^n,\; d)$ denote the graph whose vertices are the set of rational points 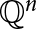$\mathbb {Q}^n$, with 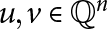$u,v \in \mathbb {Q}^n$ being adjacent if and only if the Euclidean distance between u and v is equal to d. Such a graph is deemed “non-trivial” if d is actually realized as a distance between points of 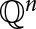$\mathbb {Q}^n$. In this paper, we show that a space 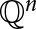$\mathbb {Q}^n$ has the property that all pairs of non-trivial distance graphs 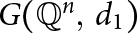$G(\mathbb {Q}^n,\; d_1)$ and 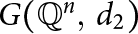$G(\mathbb {Q}^n,\; d_2)$ are isomorphic if and only if n is equal to 1, 2, or a multiple of 4. Along the way, we make a number of observations concerning the clique number of 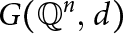$G(\mathbb {Q}^n,\; d)$.

Keywords

Euclidean distance graphrational pointsgraph isomorphismclique numberregular simplex

MSC classification

Primary: 05C62: Graph representations (geometric and intersection representations, etc.)
Secondary: 11A15: Power residues, reciprocity
Type
Article
Information
Canadian Mathematical Bulletin , Volume 64 , Issue 1 , March 2021 , pp. 13 - 24
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abrams, A. and Johnson, P. D. Jr, Yet another species of forbidden distances chromatic number. Geombinatorics 10(2001), 89–95.Google Scholar
Benda, M. and Perles, M., Colorings of metric spaces. Geombinatorics 9(2000), 113–126.Google Scholar
Brass, P., Moser, W., and Pach, J., Research problems in discrete geometry. Springer, 2005, pp. 58–59.Google Scholar
Chilakamarri, K. B., Unit-distance graphs in rational n-spaces. Discrete Math. 69(1988), 213–218. https://doi.org/10.1016/0012-365X(88)90049-0CrossRefGoogle Scholar
Chow, T., Distances forbidden by two-colorings of ${\mathbb{Q}}^3$ and An. Discrete Math. 115(1993), 95–102. https://doi.org/10.1016/0012-365X(93)90481-8CrossRefGoogle Scholar
Elsholtz, C. and Klotz, W., Maximal dimension of unit simplices. Discrete Comput. Geom. 34(2005), 167–177. https://doi.org/10.1007/s00454-004-1155-xCrossRefGoogle Scholar
Hall, M. and Ryser, H. J., Normal completion of incidence matrices. Amer. J. Math. 76 (3) (1954), 581–589. https://doi.org/10.2307/2372702CrossRefGoogle Scholar
Ionascu, E. J., A parametrization of equilateral triangles having integer coordinates. J. Integer Sequences 10(2007), #07.6.7.Google Scholar
Johnson, P. D. Jr., Two-colorings of a dense subgroup of ${\mathbb{Q}}^n$that forbid many distances. Discrete Math. 79 (1989/1990), 191–195. https://doi.org/10.1016/0012-365X(90)90033-EGoogle Scholar
Johnson, P. D. Jr., $\textit{4}={B}_\textit{1}\left({\mathbb{Q}}^\textit{3}\right)=\textit{B}_\textit{1}\left({\mathbb{Q}}^\textit{4}\right)$!. Geombinatorics 17(2008), 117–123.Google Scholar
Johnson, P. and Noble, M., A very short proof of a well-known fact about circles in the plane. Geombinatorics 25(2015), 65–69.Google Scholar
LeVeque, W. J., Fundamentals of number theory. Addison Wesley, 1977.Google Scholar
Noble, M., On 4-chromatic subgraphs of $G\left({\mathbb{Q}}^3,d\right)$. Australasian J. Comb. 65(2016), 59–70.Google Scholar
Ponomarenko, E. I. and Raigorodskii, A. M., Some analogues of the Borsuk problem in the space ${\mathbb{Q}}^n$(Russian). Dokl. Akad. Nauk 436(2011), 306–310; English translation in Dokl. Math. 83(2011), 59–62. https://doi.org/10.1134/S1064562411010182Google Scholar
Raigorodskii, A. M. and Shitova, I. M., Chromatic numbers of real and rational spaces with real or rational forbidden distances (Russian). Mat. Sb. 199(2008), 107–142; English translation in Sb. Math. 199(2008), 579–612. https://doi.org/10.1070/SM2008v199n04ABEH00934Google Scholar
Schoenberg, I. J., Regular simplices and quadratic forms. J. London Math. Soc. 12(1937), 48–55.Google Scholar
Soifer, A., The mathematical coloring book. Mathematics of coloring and the colorful life of its creators. Springer, New York, 2009.Google Scholar