Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-28T07:47:01.982Z Has data issue: false hasContentIssue false
  • English
  • Français

On Sierpinski's Conjecture Concerning the Euler Totient

Published online by Cambridge University Press:  20 November 2018

M. V. Subbarao  and
L. W. Yip
M. V. Subbarao
Affiliation:
Department of Mathematics, University of Alberta, Edmonton, Alberta, T6G 2G1
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If Φk(n) denotes the Schemmel totient (so that Φ1 (n) becomes the Euler totient) we conjecture that for each k ≥ 1 and any given integer n > 1 there exist infinitely many m for which the equation Φk(x) = m has exactly n solutions. For the case k = 1, this gives Sierpinski's conjecture.

We prove that on the basis of Schinzel's Hypothesis H, our conjecture holds for any k ≥ 3 of the form 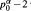where p0 is an odd prime and α ∊ N. In 1961 Schinzel proved the case k = 1 assuming his Hypothesis H.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 34 , Issue 3 , 01 September 1991 , pp. 401 - 404
Copyright
Copyright © Canadian Mathematical Society 1991

References

1. Carmichael, R. D., On Euler's ϕ-function, Bull. Amer. Math. Soc. 13 (1907), 241–143.Google Scholar
2. Carmichael, R. D., Note on Euler's ϕ -function, Bull. Amer. Math. Soc. 28 (1922), 109–110.Google Scholar
3. Erdös, P., Some remarks on Euler's φ-function, Acta Arith. 4 (1958), 10–19.Google Scholar
4. Schinzel, A., Remarks on the paper ‘Sur certaines hypothèses concernant les nombres premiers', Acta Arith. 7 (1961), 1–8.Google Scholar
5. Schinzel, A. and Sierpinski, W., Sur certaines hypothèses concernant les nombres premiers, Acta Arith. 4 (1958), 185–208.Google Scholar
6. Subbarao, M. V. and Yip, L. W., CarmichaeVs conjecture and some analogues. Proc. Int. Number Theory Conf. Univ. Laval 1987, De. Koninck and Levesque éd., Berlin: Walter de Gruyter, 1989,928–941.Google Scholar
7. Yip, L. W., On Carmichael type problems for the Schemmel totients and some related questions. Doctoral Thesis, Univ. of Alberta, 1989.Google Scholar