Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T17:30:29.859Z Has data issue: false hasContentIssue false
  • English
  • Français

On Sets of Consistent Arcs in a Tournament

Published online by Cambridge University Press:  20 November 2018

P. Erdös  and
J. W. Moon
P. Erdös
Affiliation:
University College London
J. W. Moon
Affiliation:
University College London
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

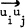A (round-robin) tournament Tn consists n of nodes u1, u2, …, un such that each pair of distinct nodes ui and uj is joined by one of the (oriented) arcs or 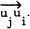The arcs in some set S are said to be consistent if it is possible to relabel the nodes of the tournament in such a way that if the arc 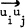is in S then i>j. (This is easily seen to be equivalent to requiring that the tournament contains no oriented cycles composed entirely of arcs of S.) Sets of consistent arcs are of interest, for example, when the tournament represents the outcome of a paired-comparison experiment [1]. The object in this note is to obtain bounds for f(n), the greatest integer k such that every tournament Tn contains a set of k consistent arcs.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 8 , Issue 3 , April 1965 , pp. 269 - 271
Copyright
Copyright © Canadian Mathematical Society 1965

References

1. Kendall, M. G. and Smith, B. Babington, On the method of paired comparisons, Biometrika, 31 (1939) 324-345.CrossRefGoogle Scholar