Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-12-03T20:00:12.503Z Has data issue: false hasContentIssue false
  • English
  • Français

On Rings of Fractions

Published online by Cambridge University Press:  20 November 2018

T. M. K. Davison
T. M. K. Davison*
Affiliation:
McMaster University, Hamilton, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R be a commutative Noetherian ring with identity, and let M be a fixed ideal of R. Then, trivially, ring multiplication is continuous in the ilf-adic topology. Let S be a multiplicative system in R, and let j = js: R → S-1R, be the natural map. One can then ask whether (cf. Warner [3, p. 165]) S-1R is a topological ring in ihe j(M)-adic topology. In Proposition 1, I prove this is the case if and only if M ⊂ p(S), where

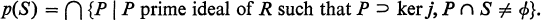
Hence S-1R is a topological ring for all S if and only if M ⊂ p*(R), where

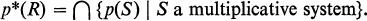
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 13 , Issue 4 , December 1970 , pp. 425 - 430
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Artin, E. and Tate, J., A note on finite ring extensions,J. Math. Soc. Japan 3 (1951), 74-77.Google Scholar
2. Gilmer, D., The pseudo-radical of a commutative ring, Pacific J. Math. 19 (1966), 275-284.Google Scholar
3. Warner, S., Compact noetherian rings, Math. Ann. 141 (1960)5 161-170.Google Scholar
4. Zariski, O. and Samuel, P., Commutative algebra I, II, Van Nostrand, Princeton, N.J., 1958.Google Scholar