Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-25T01:37:29.715Z Has data issue: false hasContentIssue false
  • English
  • Français

On Ring Properties of Injective Hulls

Published online by Cambridge University Press:  20 November 2018

N. C. Lang
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

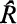Let R be an associative ring and denote by the injective hull of the right module R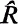R. If can be endowed with a ring multiplication which extends the existing module multiplication, we say that is a ring and the statement that R is a ring will always mean in this sense.

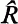It is known that is a regular ring (in the sense of von Neumann) if and only if the singular ideal of R is zero.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 18 , Issue 2 , June 1975 , pp. 233 - 239
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Hariri, H., On Infective Modules, Journal of the Math. Soc. of Japan, Vol. 21, No. 4, October 1969, pp. 574-583.Google Scholar
2. Lambek, J., Lectures on Rings and Modules, Blaisdell Publishing Co.Google Scholar
3. Matlis, E., Injective Modules over Noetherian Rings, Pacific J. of Math., 8 (1958), pp. 511-528.Google Scholar
4. Nakayama, T., On Frobeniusean Algebras, II, Ann. of Math., 42 (1941), pp. 1-21.Google Scholar
5. Osofsky, B., On Ring Properties of Injective Hulls, Canadian Math. Bull., Vol. 7, 1964, pp. 405-413.Google Scholar
6. Osofsky, B., A Generalization of Quasi-Frobenius Rings, Journal of Algebra, Vol. 4, 1966 Google Scholar