Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T06:21:21.894Z Has data issue: false hasContentIssue false
  • English
  • Français

On Relaxation Oscillations Governed by a Second Order Differential Equation for a Large Parameter and with a Piecewise Linear Function(1)

Published online by Cambridge University Press:  20 November 2018

K. K. Anand
K. K. Anand*
Affiliation:
Department of Mathematics, Concordia UniversitySir George Williams Campus, Montreal, P.Q.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper deals with the differential equation: ẍ + μF(ẋ) + x = ƒ( X, ẋ, t/Tμ) for μ ≫ 1 where F is a piecewise linear function and f is a periodic function of period μT, where T is to be chosen. It is established that periodic forced vibrations exist in an annular domain R(μ) constructed for the free vibration (ƒ ≡ 0), provided ƒ is not of higher order than 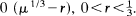Subsequently with ƒ = A cos (2πt/μT*), an asymptotic treatment of the forced vibration problem is carried out, by finding the proper initial conditions and the proper period μT* of f. Finally it is concluded that μT* is close to the period of the free vibration.

Keywords

34-0234C254E05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 26 , Issue 1 , 01 March 1983 , pp. 80 - 91
Copyright
Copyright © Canadian Mathematical Society 1983

Footnotes

(l)

This paper has been extracted from a thesis with the same title submitted and approved at Courant Institute of Mathematical Sciences, New York University, New York in 1980.

References

1. Anand, K. K., On Relaxation Oscillations Governed by a Second Order Differential Equation for a Large Parameter and with a Piecewise Linear Function, Thesis approved in 1980 by Courant Institute of Mathematical Sciences N.Y.U., available with Microfilms International or Courant Institute Library.Google Scholar
2. Doronitsyn, A. A., Asymptotic Solution of the Van der PoVs equation; A.M.S.J. Translation Series 1, 4, 1962 pp. 1-23.Google Scholar
3. Grasman, J., Veling, E. J. M. and Willems, G. M.; Relaxation Oscillations Governed by a van der Pol equation with periodic forcing term; Mathematisch Centrum Amsterdam 1975.Google Scholar
4. Haag, J., Examples Concrets d'étude asymptotique d'oscillations de rélaxation; Ann. Sci. Ecole Norm. Sup 61, 1944, pp. 73-117.Google Scholar
5. Stoker, J. J., Periodic Forced Vibrations of Systems of Relaxation Oscillators, Comm. Pure Appl. Math. Vol. XXXIII pp. 215-240 (1980).Google Scholar
6. Stoker, J. J., Non Linear Vibrations Pure and App. Maths Sciences, Vol. 2, Interscience Publishers, New York 1966; pp. 143-146.Google Scholar