Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-20T17:36:40.190Z Has data issue: false hasContentIssue false
  • English
  • Français

On Property B of Families of Sets

Published online by Cambridge University Press:  20 November 2018

H. L. Abbott  and
A. C. Liu
H. L. Abbott
Affiliation:
Department of Mathematics, The University of Alberta, Edmonton, Alberta, T6G 2G1
A. C. Liu
Affiliation:
Department of Mathematics, The University of Alberta, Edmonton, Alberta, T6G 2G1
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A family of sets is said to have property B if there exists a set S such that S∩F≠ ϕ and S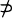F for all F 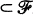. S is called a B-set for 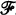. Let n≥2 and N≥2n-1. Let V = { 1, 2,≠, N} and let 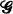= {G:G⊂ V, |G| = rc}. Erdös [3] defined mN(n) to be the size of a smallest subfamily of which does not have property B and proved the following results:

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 23 , Issue 4 , 01 December 1980 , pp. 429 - 435
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Abbott, H. L. and Moser, L.. On a combinatorial problem of Erdôs and Hajnal, Can. Math. Bull., 7 (1964), 177-181.Google Scholar
2. De Vries, H. L.. On property B and on Steiner systems, Math. Zeit., 53 (1977), 155-159.Google Scholar
3. Erdôs, P.. On a combinatorial problem III, Can. Math. Bull. 12 (1969), 413-416.Google Scholar
4. Spencer, J.. Puncture sets, J. Comb. Theory, A17 (1974), 329-336.Google Scholar
5. Stein, S. K.. Two combinatorial covering theorems, J. Comb. Theory, A16 (1974), 391-397.Google Scholar