Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T05:34:50.043Z Has data issue: false hasContentIssue false
  • English
  • Français

On Projection Bodies of Order One

Published online by Cambridge University Press:  20 November 2018

Stefano Campi  and
Paolo Gronchi
Stefano Campi
Affiliation:
Dipartimento di Ingegneria dell’Informazione, Università degli Studi di Siena, Via Roma 56, 53100 Siena, Italy e-mail: [email protected]
Paolo Gronchi
Affiliation:
Dipartimento di Matematica e Applicazioni per l’Architettura, Università degli Studi di Firenze, Piazza Ghiberti 27, 50122 Firenze, Italy e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The projection body of order one 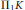${{\Pi }_{1}}K$ of a convex body 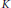$K$ in 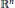${{\mathbb{R}}^{n}}$ is the body whose support function is, up to a constant, the average mean width of the orthogonal projections of 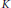$K$ onto hyperplanes through the origin.

The paper contains an inequality for the support function of 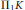${{\Pi }_{1}}K$, which implies in particular that such a function is strictly convex, unless 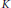$K$ has dimension one or two. Furthermore, an existence problem related to the reconstruction of a convex body is discussed to highlight the different behavior of the area measures of order one and of order 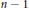$n\,-\,1$.

Keywords

52A40
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 52 , Issue 3 , 01 September 2009 , pp. 349 - 360
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Berg, Ch., Corps convexes et potentiels sphériques, Danske Vid. Selskab. Mat.-fys. Medd. 37(1969), 6.Google Scholar
[2] Bonnesen, T. and Fenchel, W., Theory of Convex Bodies, BCS Associates, Moscow, ID, 1987.Google Scholar
[3] Campi, S., Colesanti, A. and Gronchi, P., Convex bodies with extremal volumes having prescribed brightness in finitely many directions, Geom. Dedicata 57(1995), 121–133.Google Scholar
[4] Fedotov, V. P., Polar representation of a convex compactum (in Russian), Ukrain. Geom. Sb. 25(1982), 137–138.Google Scholar
[5] Firey, W. J., Christoffel's problem for general convex bodies, Mathematika 15(1968), 7–21.Google Scholar
[6] Gardner, R. J., Geometric Tomography, Cambridge University Press, New York, 2nd ed., 2006.Google Scholar
[7] Gardner, R. J. and Milanfar, P., Reconstruction of convex bodies from brightness functions, Discrete Comput. Geom. 29(2003), 279–303.Google Scholar
[8] Groemer, H., Geometric Applications of Fourier Series and Spherical Harmonics, Cambridge University Press, New York, 1996.Google Scholar
[9] Guan, P. and Ma, X. N., The Christoffel-Minkowski problem I: Convexity of solutions of a Hessian equation, Invent. Math. 151(2003), 553–577.Google Scholar
[10] Schneider, R., Über eine Integralgleichung in der Theorie der konvexen Körper, Math. Nachr. 44(1970), 55–75.Google Scholar
[11] Schneider, R., Convex bodies: The Brunn-Minkowski theory, Cambridge University Press, Cambridge, 1993.Google Scholar
[12] Schneider, R. and Weil, W., Zonoids and related topics, in Convexity and its Applications (eds Gruber P. M. and Wills G. M.), Birkhäuser, Basel (1983), 296–317.Google Scholar
[13] Weil, W., Ein Aproximationssatz für konvexe Körper, Manuscripta Math. 8(1973), 335–362.Google Scholar