Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-12-01T00:41:47.114Z Has data issue: false hasContentIssue false
  • English
  • Français

On Prime Rings with Ascending Chain Condition on Annihilator Right Ideals and Nonzero Infective Right Ideals

Published online by Cambridge University Press:  20 November 2018

Kwangil Koh  and
A. C. Mewborn
Kwangil Koh
Affiliation:
North Carolina State University, Raleigh, North Carolina
A. C. Mewborn
Affiliation:
University of North Carolina, Chapel Hill, North Carolina
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If I is a right ideal of a ring R, I is said to be an annihilator right ideal provided that there is a subset S in R such that

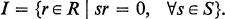
I is said to be injective if it is injective as a submodule of the right regular R-module RR. The purpose of this note is to prove that a prime ring R (not necessarily with 1) which satisfies the ascending chain condition on annihilator right ideals is a simple ring with descending chain condition on one sided ideals if R contains a nonzero right ideal which is injective.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 14 , Issue 3 , September 1971 , pp. 443 - 444
Copyright
Copyright © Canadian Mathematical Society 1971

References

1. Baer, R., Abelian groups that are direct summands of every containing Abelian group, Bull. Amer. Math. Soc. 46 (1940), 800-806.Google Scholar
2. Cartan, H. and Eilenberg, S., Homological algebra, Princeton Univ. Press, Princeton, N.J., 1956.Google Scholar
3. Divinsky, N. J., Rings and radicals, Univ. of Toronto Press, Ontario, 1965.Google Scholar
4. Johnson, R. E., Structure theory of faithful rings, III, Irreducible rings, Proc. Amer. Math. Soc. (5) 11 (1960), 710-717.Google Scholar
5. Koh, K., A note on a self-injective ring, Canad. Math. Bull. (1) 8 (1965), 29-32.Google Scholar