On Polynomials with Real Zeros

Extract

Let

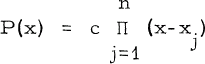
be a polynomial of degree n with real and non-negative zeros x₁ ≤ x₂ ≤ … x_n. The zeros x_j. will be said to have extent 1 if

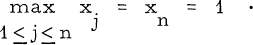
Let ξ₁ ≤ ξ₂ ≤ … ξ_n-1 be the zeros of the derived polynomial p'(x). The zeros ξ₁, ξ₂, …, ξ_n-1 are real and non-negative, and moreover their extent can be at most equal to the extent of the zeros x₁, x₂, …, x_n. The two can indeed be equal. For if the extent of the zeros x_j. is 1 and 1 is a multiple zero of p'(x) then ξ_n-1 = 1. However it is not quite clear how small ξ_n-1 = 1 can be if X_n = 1. The extent ξ_n-1 = 1. of the zeros of p'(x) is less than 1 only if 1 is not a multiple zero of p(x). So let us suppose that p(x) has a simple zero at x = 1. Consequently x_n-1 is the largest zero of p(x)/(x-l) or equivalently the largest zero of p(x) in 0 < x < 1 and it follows by Rolle's theorem that p'(x) n as a zero in the interval (x_n-1,1). Thus the extent ξ_n-1 of the zeros of p'(x) is greater than x_n-1 and it remains to see how small it can be.