Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T04:39:24.778Z Has data issue: false hasContentIssue false
  • English
  • Français

On Perturbations of Continuous Maps

Published online by Cambridge University Press:  20 November 2018

Benoît Jacob
Benoît Jacob*
Affiliation:
University of Toronto, Dept. of Mathematics, Toronto, ON M5S 2E4 e-mail: [email protected]; [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give sufficient conditions for the following problem: given a topological space 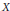$X$, a metric space 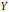$Y$, a subspace 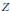$Z$ of 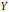$Y$, and a continuous map 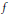$f$ from 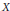$X$ to 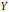$Y$, is it possible, by applying to 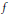$f$ an arbitrarily small perturbation, to ensure that 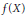$f\left( {{X}^{'}} \right)$ does not meet 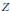$Z$? We also give a relative variant: if 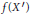$f\left( X\prime \right)$ does not meet 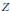$Z$ for a certain subset 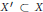${X}'\subset X$, then we may keep 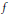$f$ unchanged on 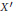${X}'$. We also develop a variant for continuous sections of fibrations and discuss some applications to matrix perturbation theory.

Keywords

54F45perturbation theorygeneral topologyapplications to operator algebras / matrix perturbation theory
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 1 , 01 March 2013 , pp. 92 - 101
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Choi, M. D. and Elliott, G. A., Density of the selfadjoint elements with finite spectrum in an irrational rotation C*-algebra. Math. Scand. 67 (1990), no. 1, 73-86.Google Scholar
[2] Engelking, R., Dimension theory. North-Holland Mathematical Library, 19, North-Holland Publishing Co., Amsterdam-Oxford-New York; PWN-Polish Scientific Publishers, Warsaw, 1978.Google Scholar
[3] Nagata, J., Modern dimension theory. Revised ed., Sigma Series in Pure Mathematics, 2, Heldermann Verlag, Berlin, 1983.Google Scholar
[4] Phillips, N. C., Simple C*-algebras with the property weak (FU). Math. Scand. 69 (1991), no. 1, 127-151.Google Scholar
[5] Phillips, N. C., How many exponentials? Amer. J. Math. 116 (1994), no. 6, 1513-1543. http://dx.doi.org/10.2307/2375057 Google Scholar