Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T18:54:10.763Z Has data issue: false hasContentIssue false
  • English
  • Français

On Nearly Equilateral Simplices and Nearly l∞ Spaces

Published online by Cambridge University Press:  20 November 2018

Gennadiy Averkov
Gennadiy Averkov*
Affiliation:
Institute for Mathematical Optimization, Faculty of Mathematics, University of Magdeburg, Magdeburg, Germany e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

By 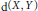$\text{d(X,Y)}$ we denote the (multiplicative) Banach–Mazur distance between two normed spaces $X$ and $Y$. Let $X$ be an $n$-dimensional normed space with 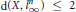$\text{d(X,}\,l_{\infty }^{n}\text{)}\,\le \,\text{2}$, where 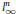$l_{\infty }^{n}$ stands for 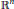${{\mathbb{R}}^{n}}$ endowed with the norm 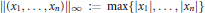$\parallel ({{x}_{1}},\,.\,.\,.\,,\,{{x}_{n}}){{\parallel }_{\infty }}\,:=\,\max \{|{{x}_{1}}|,\,.\,.\,.\,,\,|{{x}_{n}}|\}$. Then every metric space 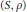$(S,\,\rho )$ of cardinality 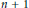$n+1$ with norm $\rho $ satisfying the condition 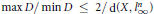$\max D/\min D\,\le \,2/\,\text{d(}X,\,l_{\infty }^{n}\text{)}$ for 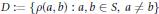$D\,:=\,\{\rho (a,\,b)\,:\,a,\,b\,\in \,S,\,a\,\ne \,b\}$ can be isometrically embedded into $X$.

Keywords

52A2151F9952C99
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 53 , Issue 3 , 01 September 2010 , pp. 394 - 397
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Averkov, G. and Düvelmeyer, N., Embedding metric spaces into normed spaces and estimates of metric capacity. Monatsh. Math. 152(2007), no. 3, 197–206. doi:10.1007/s00605-007-0472-6Google Scholar
[2] Braß, P., On equilateral simplices in normed spaces. Beiträge Algebra Geom. 40(1999), no. 2, 303–307.Google Scholar
[3] Dekster, B. V., Simplexes with prescribed edge lengths in Minkowski and Banach spaces. Acta Math. Hungar. 86(2000), no. 4, 343–358. doi:10.1023/A:1006727810727Google Scholar
[4] Gluskin, E. D., The diameter of the Minkowski compactum is roughly equal to n. Funktsional. Anal. i Prilozhen. 15(1981), no. 1, 72–73.Google Scholar
[5] Indyk, P. and Matoušek, J., Low-distortion embeddings of finite metric spaces. In: Handbook of discrete and computational geometry. Second ed., Chapman and Hall/CRC Press, Boca Raton, FL, 2004, pp. 177–196.Google Scholar
[6] Lindenstrauss, J. and Milman, V. D., The local theory of normed spaces and its applications to convexity. In: Handbook of convex geometry, Vol. A, B, North-Holland, Amsterdam, 1993, pp. 1149–1220.Google Scholar
[7] Matoušek, J., Lectures on discrete geometry. Graduate Texts in Mathematics, 212, Springer-Verlag, New York, 2002.Google Scholar
[8] Munkres, J. R., Elements of algebraic topology. Addison-Wesley, Menlo Park, CA, 1984.Google Scholar
[9] Schoenberg, I. J., Metric spaces and positive definite functions. Trans. Amer. Math. Soc. 44(1938), no. 3, 522–536. doi:10.2307/1989894Google Scholar
[10] Swanepoel, K. J. and Villa, R., A lower bound for the equilateral number of normed spaces. Proc. Amer. Math. Soc. 136(2008), no. 1, 127–131. doi:10.1090/S0002-9939-07-08916-2Google Scholar