No CrossRef data available.
Article contents
On Mertens' Theorem for Beurling Primes
Published online by Cambridge University Press: 20 November 2018
Abstract.
Let 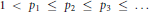 $1\,<\,{{p}_{1}}\,\le \,{{p}_{2}}\,\le \,{{p}_{3}}\,\le \,...$ be an infinite sequence
$1\,<\,{{p}_{1}}\,\le \,{{p}_{2}}\,\le \,{{p}_{3}}\,\le \,...$ be an infinite sequence 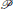 $P$ of real numbers for which
$P$ of real numbers for which 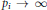 ${{p}_{i}}\,\to \,\infty $, and associate with this sequence the Beurling zeta function
${{p}_{i}}\,\to \,\infty $, and associate with this sequence the Beurling zeta function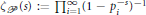 $\zeta P\left( s \right)\,:=\,{{\prod\nolimits_{i=1}^{\infty }{\left( 1\,-\,p_{i}^{-s} \right)}}^{-1}}$. Suppose that for some constant
$\zeta P\left( s \right)\,:=\,{{\prod\nolimits_{i=1}^{\infty }{\left( 1\,-\,p_{i}^{-s} \right)}}^{-1}}$. Suppose that for some constant 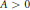 $A\,>\,0$, we have
$A\,>\,0$, we have 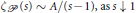 $\zeta P\left( s \right)\tilde{\ }A/\left( s-1 \right),\ \text{as}\,s\,\downarrow \,1$. We prove that
$\zeta P\left( s \right)\tilde{\ }A/\left( s-1 \right),\ \text{as}\,s\,\downarrow \,1$. We prove that 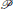 $P$ satisfies an analogue of a classical theorem of Mertens:
$P$ satisfies an analogue of a classical theorem of Mertens: 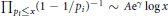 ${{\prod{_{{{p}_{i}}\le x}\left( 1\,-\,{1}/{{{p}_{i}}}\; \right)}}^{-1}}\,\sim \,A{{\text{e}}^{\gamma }}\,\log \,x$, as
${{\prod{_{{{p}_{i}}\le x}\left( 1\,-\,{1}/{{{p}_{i}}}\; \right)}}^{-1}}\,\sim \,A{{\text{e}}^{\gamma }}\,\log \,x$, as 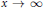 $x\,\to \,\infty $. Here
$x\,\to \,\infty $. Here 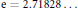 $\text{e}\,\text{=}\,\text{2}\text{.71828}...$ is the base of the natural logarithm and
$\text{e}\,\text{=}\,\text{2}\text{.71828}...$ is the base of the natural logarithm and  $\gamma \,=\,0.57721...$ is the usual Euler–Mascheroni constant. This strengthens a recent theorem of Olofsson.
$\gamma \,=\,0.57721...$ is the usual Euler–Mascheroni constant. This strengthens a recent theorem of Olofsson.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2013


