No CrossRef data available.
Article contents
On meromorphic solutions of certain partial differential equations
Part of:
Entire and meromorphic functions, and related topics
General first-order equations and systems
Holomorphic functions of several complex variables
Published online by Cambridge University Press: 24 March 2025
Abstract
In this article, we describe meromorphic solutions of certain partial differential equations, which are originated from the algebraic equation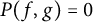 
$P(f,g)=0$, where P is a polynomial on 
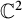$\mathbb {C}^2$. As an application, with the theorem of Coman–Poletsky, we give a proof of the classic theorem: Every meromorphic solution 
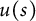$u(s)$ on 
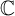$\mathbb {C}$ of 
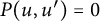$P(u,u')=0$ belongs to W, which is the class of meromorphic functions on 
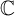$\mathbb {C}$ that consists of elliptic functions, rational functions and functions of the form 
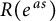$R(e^{a s})$, where R is rational and 
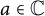$a\in \mathbb {C}$. In addition, we consider the factorization of meromorphic solutions on 
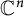$\mathbb {C}^n$ of some well-known PDEs, such as Inviscid Burgers’ equation, Riccati equation, Malmquist–Yosida equation, PDEs of Fermat type.
- Type
- Article
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society
Footnotes
This work was supported by Natural Science Foundation of Shandong Province (ZR2022MA014).
References
Brownawell, W. D.,
On the factorization of partial differential equations
. Can. J. Math. 39(1987), 825–834.Google Scholar
Briot, C. H. and Bouquet, J., Théorie des fonctions doublement périodiques et, en particulier, desfonctions elliptiques. Mallet-Bachelier, Paris, 1859.Google Scholar
Briot, C. H. and Bouquet, J.,
Intégration des équations différentielles au moyen de fonctions elliptiques
. J. Ecole Polytech. 21(1856), 199–254.Google Scholar
Chang, D. C., Li, B. Q., and Yang, C. C.,
On composition of meromorphic functions in several complex variables
. Forum Math. 7(1995), 77–94.Google Scholar
Coman, D. and Poletsky, E. A.,
Stable algebras of entire functions
. Proc. Amer. Math. Soc. 136(2008), 3993–4002.Google Scholar
Eremenko, A.,
Meromorphic solutions of equations of Briot-Bouquet type
. Teor. Funktsii, Funk. Anal. i Prilozh. 38(1982), 48–56. English translation: Amer. Math. Soc. Trans.l 133(1986), 15–23.Google Scholar
Eremenko, A., Liao, L. W., and Ng, T. W.,
Meromorphic solutions of higher order Briot-Bouquet differential equations
. Math. Proc. Cambridge Philos. Soc. 146(2009), 197–206.Google Scholar
Edrei, A. and Fuchs, W. H. J., On thc zeros of
$f\left(g(z)\right)$
, where
$f$
and
$g$
are entire functions. J. Anal. Math. 12(1964), 243–255.Google Scholar
$f\left(g(z)\right)$
, where
$f$
and
$g$
are entire functions. J. Anal. Math. 12(1964), 243–255.Google ScholarGreen, M.,
Some Picard theorems for holomorphic maps to algebraic varieties
. Amer. J. Math. 97(1975), 43–75.Google Scholar
Gross, F.,
On factorization of meromorphic functions
. Trans. Amer. Math. Soc. 131(1968), 215–222.Google Scholar
Gross, F., Yang, C. C., and Osgood, C.,
Primeable entire functions
. Nagoya Math J. 51(1973), 123–130.Google Scholar
Hille, E.,
Higher order Briot-Bouquet differential equations
. Ark. Mat. 16(1978), 271–286.Google Scholar
Hille, E.,
Remarks on Briot-Bouquet differential equations I
. Comment. Math. 1(1978), 119–132.Google Scholar
Hille, E.,
Some remarks on Briot-Bouquet differential equations II
. J. Math. Anal. Appl. 65(1978), 572–585.Google Scholar
Hu, P. C. and Yang, C. C.,
Malmquist type theorem and factorization of meromorphic solutions of partial differential equations
. Complex Var., Theory Appl. 27(1995), 269–285.Google Scholar
Kujala, R. O.,
Functions of finite-type in several complex variables
. Trans. Amer. Math. Soc. 161(1971), 327–358.Google Scholar
Liao, L. W. and Yang, C. C.,
On the growth and factorization of entire solutions of algebraic differential equations
. Ann. Acad. Sci. Fenn. Math. 25(2000), 73–84.Google Scholar
Li, B. Q.,
Entire solutions of certain partial differential equations and factorization of partial derivatives
. Trans. Amer. Math. Soc. 357(2004), 3169–3177.Google Scholar
Li, B. Q.,
Entire solutions of certain partial differential equations in
${\mathbb{C}}^n$
. Isr. J. Math. 143(2004), 131–140.Google Scholar
${\mathbb{C}}^n$
. Isr. J. Math. 143(2004), 131–140.Google ScholarLi, B. Q. and Saleeby, E. G.,
Entire solutions of first-order partial differential equations
. Complex Var., Theory Appl. 48(2003), 657–661.Google Scholar
Rosenbloom, P. C.,
The fix-points of entire functions
. Med. Lunds Univ. Mat. Sem. Suppl. Bd. M. Riesz. 186(1952), 186–192.Google Scholar
Saleeby, E. G.,
On complex analytic solutions of certain trinomial functional and partial differential equations
. Aequ. Math. 85(2013), 553–562.Google Scholar
Saleeby, E. G.,
Meromorphic solutions of generalized inviscid Burgers’ equations and a family of quadratic PDEs
. J. Math. Anal. Appl. 425(2015), 508–519.Google Scholar
Saleeby, E. G.,
On meromorphic solutions of first-order Briot-Bouquet type PDEs
. J. Math. Anal. Appl. 482(2020), 123517.Google Scholar
Strelitz, Sh.,
Three theorems on the growth of entire transcendental solutions of algebraic differential equations
. Can J. Math. 35(1983), 1110–1128.Google Scholar
Steinmetz, N.,
Über die Faktorisierbaren Losungen gewöhnlicher differential Gleichungen
. Math. Z. 170(1980), 169–180.Google Scholar
Tu, Z. H.,
On meromorphic solutions of some algebraic partial differential equations on
${\mathbb{C}}^n$
. J. Math. Anal. Appl. 214(1997), 1–10.Google Scholar
${\mathbb{C}}^n$
. J. Math. Anal. Appl. 214(1997), 1–10.Google ScholarVitter, A.,
The lemma of the logarithmic derivative in seveal complex variables
. Duke Math. J. 44(1977), 89–104.Google Scholar
Zimogljad, V. V.,
On the growth of entire transcendental solutions of second-order algebraic differential equations
. Math. USSR Sb. 14(1971), 281–296.Google Scholar