Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lawruk, Bohdan
and
Światak, Halina
1974.
On functions satisfying a generalized mean value equation.
Aequationes Mathematicae,
Vol. 11,
Issue. 1,
p.
1.


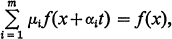
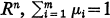 , and Σ
, and Σ