Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T19:26:44.251Z Has data issue: false hasContentIssue false
  • English
  • Français

On Lattice Analogues of Absolutely Summing Constants*

Published online by Cambridge University Press:  20 November 2018

J. Szulga
J. Szulga*
Affiliation:
Institute of Mathematics, Wrocław, University50-384 Wrocław, Poland
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let E be a Banach lattice,

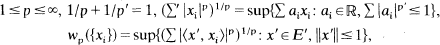
where x1, …, xn ∊ E. We study properties of constants

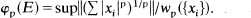
A characterization of AM-spaces is obtained which generalizes the result of Abramocič, Positselskiĭ, Yanovskii. Asymptotic estimates of φp for some classical finite dimensional lattices are given.

Keywords

46B3060B99
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 26 , Issue 1 , 01 March 1983 , pp. 63 - 69
Copyright
Copyright © Canadian Mathematical Society 1983

Footnotes

Acknowledgement. The author wishes to thank Professor W. A. Woyczynski for his attention and for the help in the redaction of this paper.

*

The research for this paper was begun when the author was a guest of the Cleveland State University, Ohio, U.S.A.

References

1. Abramovič, Y., Some theorems on normed lattices, Véstnik Leningrad Univ. Math., 4 (1977), 153-159.Google Scholar
2. Abramovič, Y. A., Positselskiǐ, E. D. and Yanovskiǐ, L. P., On some parameters associated with normed lattices and on series characterization of M-spaces, Studia Math., LXIII (1978), 1-8.Google Scholar
3. Gordon, Y., On p-absolutely summing constants of Banach spaces, Israel J. Math., 7 (1969), 151-163.Google Scholar
4. Kakutani, S., Concrete representation of abstract M-spaces, Ann. of Math., 42 (1941), 994-1024.Google Scholar
5. Krivine, J. L., Théorèmes de factorization dans les espaces réticules, Séminaire Maurey-Schwartz, (1973-1974), Exp. XXII, XXIII.Google Scholar
6. Mcphail, M. S., Absolute and unconditional convergence, Bull. Amer. Math. Soc., 53 (1947), 121-123.Google Scholar
7. Schaeffer, H. H., Banach lattices and Positive Operators, Springer Vg, Berlin, 1974.Google Scholar
8. Szulga, J., Lattice moments of random vectors, Bull. Pol. Acad. Scie., XXVIII, No 1–2, (1980), 87-93.Google Scholar
9. Szulga, J., On operator characterization of AM- and Ah-spaces, Proc. Conf. “Probability on vector spaces“, Błażeievko 1979, Lecture Notes in Maths. No 828, Springer Vg, 277-282.Google Scholar