Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T07:56:01.589Z Has data issue: false hasContentIssue false
  • English
  • Français

On Incomplete Character Sums to a Prime-Power Modulus

Published online by Cambridge University Press:  20 November 2018

J. H. H. Chalk
J. H. H. Chalk*
Affiliation:
University of Toronto, Toronto, Ont. M5S 1A1
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let x denote a primitive character to a prime-power modulus k = pα. The expected estimate

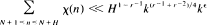
for the incomplete character sum has been established for r = 1 and 2 by D. A. Burgess and recently, he settled the case r = 3 for all primes p < 3, (cf. [2] for the proof and for references). Here, a short proof of the main inequality (Theorem 2) which leads to this result is presented; the argument being based upon my characterization in [3] of the solution-set of a related congruence.

Keywords

10A1010G05CongruencesCharacter Sums
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 30 , Issue 3 , 01 September 1987 , pp. 257 - 266
Copyright
Copyright © Canadian Mathematical Society 1987

References

1. Burgess, D.A., On Character Sums and L-series, Proc. London Math. Soc, (3), 12 (1962), pp. 193–206.Google Scholar
2. Burgess, D.A., Estimation of Character Sums Modulo a Power of a prime, ibid (3) 52 (1986), pp. 215–235.Google Scholar
3. Chalk, J.H.H., On a Congruence related to Character Sums, Canadian Math. Bull., 28(4) (1985), pp. 431–439.Google Scholar
4. Hua, L.-K., Enzyklopädie der Mat. Wissenschaften, Band 12, Heft 13, Teil 1; B.13.Google Scholar
5. Hua, L.-K., Additive Primzahltheorie, (Teubner, Leipzig), 1959.Google Scholar