Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T18:31:07.799Z Has data issue: false hasContentIssue false
  • English
  • Français

On Hodge Theory of Singular Plane Curves

Published online by Cambridge University Press:  20 November 2018

Nancy Abdallah
Nancy Abdallah*
Affiliation:
Univ. Nice Sophia Antipolis, CNRS, LJAD, UMR 7351, 06100 Nice, France e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The dimensions of the graded quotients of the cohomology of a plane curve complement 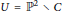$U\,=\,{{\mathbb{P}}^{2}}\,\backslash \,C$ with respect to the Hodge filtration are described in terms of simple geometrical invariants. The case of curves with ordinary singularities is discussed in detail. We also give a precise numerical estimate for the difference between the Hodge filtration and the pole order filtration on 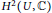${{H}^{2}}\left( U,\,\mathbb{C} \right)$.

Keywords

32S3532S2214H50plane curvesHodge and pole order filtrations
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 3 , 01 September 2016 , pp. 449 - 460
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Abdallah, N., On plane curves with double and triple points. MathematicaScandinavica, to appear. arxiv:1401.6032Google Scholar
[2] Deligne, P., Théorie de Hodge II. Inst. Hautes Études Sci. Publ. Math. 40(1971), 5–57.Google Scholar
[3] Deligne, P. and Dimca, A., Filtrations de Hodge et par l'ordre du pôle pour les hypersurfaces singulières. Ann. Sci. École Norm. Sup. (4) 23(1990), no. 4, 645–656.Google Scholar
[4] Dimca, A., Singularities and topology hypersurfaceUniversitext, Springer-Verlag, New York, 1992. http://dx.doi.org/10.1007/978-1-4612-4404-2 Google Scholar
[5] Dimca, A. and Saito, M., A Generalization on Griffiths’ theorem on rational integrals.Duke Math. J. 135(2006), no. 2,303-326. http://dx.doi.org/10.1215/S0012-7094-06-13523-8 Google Scholar
[6] Dimca, A. and Sernesi, E., Syzygies and logarithmic vector fields along plane curves. J. Éc. polytech. Math. 1(2014), 247–267. http://dx.doi.org/10.5802/jep.10 Google Scholar
[7] Dimca, A. and Sticlaru, G., Chebyshev curves, free resolutions and rational curve arrangements. Math. Proc. Cambridge Philos. Soc. 153(2012), no. 3, 385–397. http://dx.doi.org/10.1017/S0305004112000138 Google Scholar
[8] Dimca, A. and Sticlaru, G., Koszul complexes and pole order filtrations. Proc. Edinburgh Math. Soc. 58(2015), no. 2, 333–354. http://dx.doi.org/10.101 7/S0013091 5140001 82 Google Scholar
[9] Dimca, A. and Sticlaru, G., Hessian ideals of a homogeneous polynomial and generalized Tjurina algebras.Doc. Math. 20(2015), 689–705.Google Scholar
[10] Griffiths, P. A., On the period of certain rational integrals I, II. Ann. of Math. 90(1969), 460-495; 496–541.Google Scholar
[11] Milnor, J., Singular points of complex hypersurfaces. Annals of Mathematics Studies, 61, Princeton University Press, Princeton, NJ; University of Tokyo Press, Tokyo, 1968.Google Scholar
[12] Saito, M., On b-function, spectrum and rational singularity. Math. Ann. 295(1993), no. 1, 51–74. http://dx.doi.org/10.1007/BF01444876 Google Scholar
[13] Sernesi, E., The local cohomology of the facobian ring. Doc. Math. 19(2014), 541–565.Google Scholar
[14] Vallès, J., Free divisors in a pencil of curves. J. Singul. 11(2015), 190–197.Google Scholar
[15] Voisin, C., Théorie de Hodge et Géométrie algébrique complexe. Cours Spécialisés, 10, Société Mathématique de France, Paris, 2002. http://dx.doi.org/!0.1017/CBO9780511615344 Google Scholar