Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-28T05:09:49.751Z Has data issue: false hasContentIssue false
  • English
  • Français

On Harmonic Theory in Flows

Published online by Cambridge University Press:  20 November 2018

Hong Kyung Pak
Hong Kyung Pak*
Affiliation:
Department of Mathematics Kyungsan University Kyungsan City 712-240 Korea, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Recently [8], a harmonic theory was developed for a compact contact manifold from the viewpoint of the transversal geometry of contact flow. A contact flow is a typical example of geodesible flow. As a natural generalization of the contact flow, the present paper develops a harmonic theory for various flows on compact manifolds. We introduce the notions of 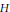$H$-harmonic and 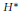${{H}^{*}}$-harmonic spaces associated to a Hörmander flow. We also introduce the notions of basic harmonic spaces associated to a weak basic flow. One of our main results is to show that in the special case of isometric flow these harmonic spaces are isomorphic to the cohomology spaces of certain complexes. Moreover, we find an obstruction for a geodesible flow to be isometric.

Keywords

53C2057R30contact structuregeodesible flowisometric flowbasic cohomology
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 46 , Issue 4 , 01 December 2003 , pp. 617 - 631
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Carriére, Y., Flots riemannienes. Astérisque 116 (1984), 31–52.Google Scholar
[2] Dominguez, D., Finiteness and tenseness for Riemannian foliations. Preprint.Google Scholar
[3] El Kacimi-Alaoui, A. and Hector, G., Décomposition de Hodge basique pour un feuilletage riemannien. Ann. Inst. Fourier 36 (1986), 207–227.Google Scholar
[4] Kitahara, H., Differential geometry of Riemannian foliations. Kyungpook Nat. Univ., 1986.Google Scholar
[5] March, P., Min-Oo, M. and Ruh, R. A., Mean curvature of Riemannian foliations. Canad. Math. Bull. 39 (1996), 95–105.Google Scholar
[6] Molino, P. and Sergiescu, V., Deux remarques sur les fiots riemanniens. Manuscripta Math. 51 (1985), 145–161.Google Scholar
[7] Ogawa, Y., On C-harmonic forms in a compact Sasakian space. Tohoku Math. J. 19 (1967), 267–296.Google Scholar
[8] Pak, H. K. and Takahashi, T., Harmonic forms in a compact contact manifold. Tohoku Math. Publ. 20 (2001), 125–138.Google Scholar
[9] Reinhart, B., Harmonic integrals on foliated manifolds. Amer. J. Math. 91 (1959), 529–536.Google Scholar
[10] Rumin, M., Un complexe de formes différentielles sur les variétés de contact. C. R. Acad. Sci. Paris 310 (1990), 401–404.Google Scholar
[11] Rumin, M., Formes différentielles sur les variétés de contact. J. Differential Geom. 39 (1994), 281–330.Google Scholar
[12] Saralegui, M., The Euler class for flows of isometries. Pitman Res. Notes inMath. 131 (1985), 220–227.Google Scholar
[13] Sasaki, S., On differentiable manifolds with certain structures which are closely related to almost contact structure. Tohoku Math. J. 12 (1960), 459–476.Google Scholar
[14] Tachibana, S., On a decomposition of C-harmonic forms in a compact Sasakian space. Tohoku Math. J. 19 (1967), 198–212.Google Scholar
[15] Tanno, S., Harmonic forms and Betti numbers of certain contact Riemannian manifolds. J. Math. Soc. Japan 19 (1967), 308–316 Google Scholar
[16] Tondeur, Ph., Foliations on Riemannian manifolds. Universitext, Springer, New York, 1988.Google Scholar