Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T20:47:54.810Z Has data issue: false hasContentIssue false
  • English
  • Français

On GL2 of a Local Ring in Which 2 is Not a Unit

Published online by Cambridge University Press:  20 November 2018

A. W. Mason
A. W. Mason*
Affiliation:
Department of Mathematics the University Glasgow, G12 8QW
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A be a local ring with maximal ideal m, let N(m ) be the order of the residue field A/m and let N be a subgroup of GLn (A) which is normalized by SLn(A). It follows from results of Klingenberg that N is normal in GLn(A) when n ≥ 3 or 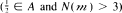. Results of Lacroix show that this is also true when n = 2 and N(m) = 3, provided that N∩2(A) ≠ SL2(A)'.

The principal aim of this paper is to provide examples of non-normal subgroups of GL2(A) which are normalized by SL2(A). In the process we extend results of Lacroix and Levesque on GL2(A)-normalized subgroups of GL2(A), where 2 ∊ m and N(m) > 2.

Keywords

20 H 05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 30 , Issue 2 , 01 June 1987 , pp. 165 - 176
Copyright
Copyright © Canadian Mathematical Society 1987

References

1. Klingenberg, W., Lineare Gruppen über lokalen Ringen, Amer. J. Math. 83 (1961), pp. 137—153.Google Scholar
2. Lacroix, N. H.J., Two-dimensional linear groups over local rings, Canad. J. Math. 21 (1969), pp. 106–135.Google Scholar
3. Lacroix, N. H.J. and Levesque, C., Sur les sous-groupes normaux de SL2 sur un anneau local, Canad. Math. Bull. 26(2) (1983), pp. 209–219.Google Scholar
4. McQuillan, D.L., Classification of normal congruence subgroups of the modular group, Amer. J. Math. 87(1965), pp. 285–296.Google Scholar
5. Mason, A.W., On subgroups of GL(n, A) which are generated by commutators II, J. Reine Angew. Math. 322(1981), pp. 118–135.Google Scholar
6. Mason, A.W., Anomalous normal subgroups of the modular group, Comm. Algebra 11 (1983), pp. 2555–2573.Google Scholar