Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-30T15:40:33.182Z Has data issue: false hasContentIssue false
  • English
  • Français

On Functional Representations of a Ring without Nilpotent Elements

Published online by Cambridge University Press:  20 November 2018

Kwangil Koh
Kwangil Koh*
Affiliation:
Tulane University, New Orleans, Louisiana; North Carolina State University, Raleigh, North Carolina
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

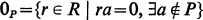In [3, p. 149], J. Lambek gives a proof of a theorem, essentially due to Grothendieck and Dieudonne, that if R is a commutative ring with 1 then R is isomorphic to the ring of global sections of a sheaf over the prime ideal space of R where a stalk of the sheaf is of the form R/0P, for each prime ideal P, and . In this note we will show, this type of representation of a noncommutative ring is possible if the ring contains no nonzero nilpotent elements.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 14 , Issue 3 , September 1971 , pp. 349 - 352
Copyright
Copyright © Canadian Mathematical Society 1971

References

1. Dauns, J. and Hofmann, K. H., Representation of rings by sections, Memoirs Amer. Math. Soc, 83, 1968.Google Scholar
2. Koh, K., A note on a certain class of prime rings, Amer. Math. Monthly, 72, 1965.Google Scholar
3. Lambek, J., Lectures on rings and modules, Blaisdell, Waltham, Mass., 1966.Google Scholar
4. Pierce, R. S., Modules over commutative regular rings, Memoirs Amer. Math. Soc, 70. 1967.Google Scholar
5. Stewart, P. N., Semi-simple radical classes, Pacific J. Math. 32 (1970), 249-254.Google Scholar